如图,已知抛物线 $C_1:y=\dfrac14x^2$,圆 $C_2:x^2+\left(y-1\right)^2=1$,过点 $P\left(t,0\right)$($t>0$)作不过原点 $O$ 的直线 $PA$,$PB$ 分别与抛物线 $C_1$ 和圆 $C_2$ 相切,$A$,$B$ 为切点.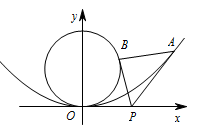

【难度】
【出处】
2015年高考浙江卷(文)
【标注】
-
求点 $A$,$B$ 的坐标;标注答案$A\left(2t,t^2\right)$.
$B\left(\dfrac{2t}{1+t^2},\dfrac{2t^2}{1+t^2}\right)$.解析本题把相切的条件合理地表达出来即可求解.其中抛物线的切线可以考虑直线与抛物线联立后用判别式,也可以用导数;圆的切线可以巧妙地利用点 $B$ 和点 $O$ 关于圆心对称来构造条件.由题意知直线 $PA$ 的斜率存在,故可设直线 $PA$ 的方程为 $y=k\left(x-t\right)$.
由 $\begin{cases}
y=k\left(x-t\right),\\
y=\dfrac 14x^2
\end{cases}$ 消去 $y$,整理得 $x^2-4kx+4kt=0$.
由于直线 $PA$ 与抛物线相切,所以\[\Delta=16k^2-16kt=0,\]由题意知 $k\ne 0$,于是可得 $k=t$.
此时,方程 $x^2-4kx+4kt=0$ 的解为\[x=2t.\]即点 $A$ 的横坐标为 $2t$,因此,点 $A$ 的坐标为\[\left(2t,t^2\right).\]设圆 $C_2$ 的圆心为 $D\left(0,1\right)$,点 $B$ 的坐标为 $\left(x_0,y_0\right)$.
由题意知点 $B$,$O$ 关于直线 $PD$ 对称,且直线 $PD$ 的方程为\[y-1=-\dfrac 1tx.\]故 $\begin{cases}
\dfrac{y_0}2\overset{\left[a\right]}=-\dfrac{x_0}{2t}+1,\\
\dfrac{y_0}{x_0}\left(-\dfrac 1t\right)\overset{\left[b\right]}=-1,
\end{cases}$(推导中用到:[a][b])解得 $\begin{cases}x_0=\dfrac{2t}{1+t^2},\\
y_0=\dfrac{2t^2}{1+t^2},
\end{cases}$
因此,点 $B$ 的坐标为 $\left(\dfrac{2t}{1+t^2},\dfrac{2t^2}{1+t^2}\right)$. -
求 $\triangle PAB$ 的面积.
注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切,称该公共点为切点.标注答案$\dfrac{t^3}2$.解析按照弦长公式和点到直线距离公式表达面积即可.由两点间距离公式得\[{\left|{AP}\right|}=\sqrt{\left(2t-t\right)^2+\left(t^2-0\right)^2}=t\cdot \sqrt{1+t^2},\]直线 $PA$ 的方程为\[tx-y-t^2=0.\]点 $B$ 到直线 $PA$ 的距离是\[d=\dfrac{t^2}{\sqrt{1+t^2}}.\]设 $\triangle PAB$ 的面积为 $S\left(t\right)$,则 $S\left(t\right)=\dfrac 12 {\left|{AP}\right|} \cdot d=\dfrac{t^3}2$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2