《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马 $P-ABCD$ 中,$侧棱PD\perp 底面ABCD$,且 $PD
=CD$,点 $E$ 是 $PC$ 的中点,连接 $DE$,$BD$,$BE$.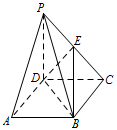
=CD$,点 $E$ 是 $PC$ 的中点,连接 $DE$,$BD$,$BE$.

【难度】
【出处】
2015年高考湖北卷(文)
【标注】
-
证明:$DE\perp 平面PBC$.试判断四面体 $EBCD$ 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由.标注答案略解析本题需要先理解鳖臑的概念,然后证明垂直即可.因为 $PD\perp 底面ABCD$,
所以 $PD\perp BC$.
由底面 $ABCD$ 为长方形,有 $BC\perp CD$,
而 $PD\cap CD=D$,
所以 $BC\perp 平面PCD$.
因为 $DE\subset 平面PCD$,
所以 $BC\perp DE$.
又因为 $PD=CD$,点 $E$ 是 $PC$ 的中点,
所以 $DE\perp PC$.
而 $PC\cap BC=C$,
所以 $DE\perp 平面PBC$.
由 $BC\perp 平面PCD$,$DE\perp 平面PBC$,可知四面体 $EBCD$ 的四个面都是直角三角形,即四面体 $EBCD$ 是一个鳖臑,其四个面的直角分别为 $\angle BCD$,$\angle BCE$,$\angle DEC$,$\angle DEB$. -
记阳马 $P-ABCD$ 的体积为 $V_1$,四面体 $EBCD$ 的体积为 $V_2$,求 $\dfrac{V_1}{V_2}$ 的值.标注答案$4 $解析本题分别把两个几何体的体积表示出来,然后求比值即可.由已知,$PD$ 是阳马 $P-ABCD$ 的高,所以 $P-ABCD$ 的体积\[V_1=\dfrac 13S_{长方形ABCD}\cdot PD=\dfrac 13BC\cdot CD\cdot PD .\]由 $(1)$ 知,$DE$ 是鳖臑 $D-BCE$ 的高,$BC\perp CE$,所以 $EBCD$ 的体积\[V_2=\dfrac 13S_{\triangle BCE}\cdot DE=\dfrac 16BC\cdot CE\cdot DE .\]在 $\mathrm {Rt}\triangle PDC$ 中,因为 $PD=CD$,点 $E$ 是 $PC$ 的中点,所以 $DE=CE=\dfrac{\sqrt 2}2 CD$,于是\[\dfrac{V_1}{V_2}=\dfrac{\dfrac 13BC\cdot CD\cdot PD}{\dfrac 16BC\cdot CE\cdot DE}=\dfrac{2CD\cdot PD}{CE\cdot DE}=4 .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2