一种作图工具如图 ① 所示．$O$ 是滑槽 $AB$ 的中点，短杆 $ON$ 可绕 $O$ 转动，长杆 $MN$ 通过 $N$ 处铰链与 $ON$ 连接，$MN$ 上的栓子 $D$ 可沿滑槽 $AB$ 滑动，且 $DN=ON=1$，$MN=3$．当栓子 $D$ 在滑槽 $AB$ 内作往复运动时，带动 $N$ 绕 $O$ 转动一周（$D$ 不动时，$N$ 也不动），$M$ 处的笔尖画出的曲线记为 $C$．以 $O$ 为原点，$AB$ 所在的直线为 $x$ 轴建立如图 ② 所示的平面直角坐标系．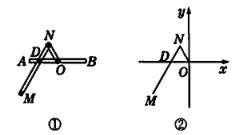
【难度】
【出处】
无
【标注】
-
求曲线 $C$ 的方程；标注答案$\dfrac{x^2}{16}+\dfrac{y^2}4=1$．解析本题利用相关点法求轨迹即可，注意点的坐标之间的关系．设 $N\left(x_0,y_0\right)$，则 $D\left(2x_0,0\right)\left(|x_0|\leqslant 1\right)$，$M\left(x,y\right)$，依题意\[{\left|{\overrightarrow{ON}}\right|}=\sqrt{x_0^2+y_0^2}=1,\]又 $\overrightarrow{MD}=2\overrightarrow{DN}$，所以\[\left(2x_0-x,-y\right)=2\left(-x_0,y_0\right),\]即\[\begin{cases}x=4x_0,\\y=-2y_0.\end{cases}\]代入 $x_0^2+y_0^2=1$，可得\[\dfrac{x^2}{16}+\dfrac{y^2}4=1,\]即所求的曲线 $C$ 的方程为 $\dfrac{x^2}{16}+\dfrac{y^2}4=1$．
-
设动直线 $l$ 与两定直线 $l_1:x-2y=0$ 和 $l_2:x+2y=0$ 分别交于 $P$，$Q$ 两点．若直线 $l$ 总与曲线 $C$ 有且只有一个公共点，试探究：$\triangle OPQ$ 的面积是否存在最小值？若存在，求出该最小值；若不存在，说明理由．标注答案$8$解析本题把直线 $l$ 方程设出后，根据直线与椭圆相切的条件找到关系，然后表示出 $PQ$ 的长和原点到直线 $l$ 的距离，就可以表示出三角形 $OPQ$ 的面积了．（i）当直线 $l$ 的斜率不存在时，直线 $l$ 为 $x=4$ 或 $x=-4$，都有 $S_{\triangle OPQ}=\dfrac 12\times 4\times 4=8$．
（ii）当直线 $l$ 的斜率存在时，设直线 $l:y=kx+m\left(k\neq \pm\dfrac 12\right)$，
由 $\begin{cases}
y=kx+m,\\
x^2+4y^2=16,
\end{cases}$ 消去 $y$，可得\[\left(1+4k^2\right)x^2+8kmx+4m^2-16=0.\]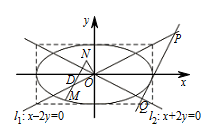
因为直线 $l$ 总与椭圆 $C$ 有且只有一个公共点，所以\[\Delta=64k^2m^2-4\left(1+4k^2\right)\left(4m^2-16\right)=0 ,\]即\[m^2=16k^2+4. \quad \cdots \cdots ① \]又由 $\begin{cases}
y=kx+m,\\
x-2y=0,
\end{cases}$ 可得 $P\left(\dfrac{2m}{1-2k},\dfrac{m}{1-2k}\right)$；同理可得 $Q\left(\dfrac{-2m}{1+2k},\dfrac{m}{1+2k}\right)$．
由原点 $O$ 到直线 $PQ$ 的距离为 $d=\dfrac{|m|}{\sqrt{1+k^2}}$和 ${\left|{PQ}\right|}=\sqrt{1+k^2} {\left|{x_P-x_Q}\right|}$，可得\[\begin{split}S_{\triangle OPQ}&=\dfrac 12 {\left|{PQ}\right|}\cdot d\\&=\dfrac 12 {\left|{m}\right|} {\left|{x_P-x_Q}\right|}\\&=\dfrac 12\cdot {\left|{m}\right|}\cdot {\left|{\dfrac{2m}{1-2k}+\dfrac{2m}{1+2k}}\right|}\\&={\left|{\dfrac{2m^2}{1-4k^2}}\right|}. \quad \cdots \cdots ② \end{split}\]将 $ ① $ 代入 $ ② $，得\[S_{\triangle OPQ}={\left|{\dfrac{2m^2}{1-4k^2}}\right|}=8\dfrac{|4k^2+1|}{|4k^2-1|} .\]当 $k^2>\dfrac 14$ 时，\[S_{\triangle OPQ}=8\left(\dfrac{4k^2+1}{4k^2-1}\right)=8\left(1+\dfrac{2}{4k^2-1}\right)>8;\]当 $0\leqslant k^2<\dfrac 14$ 时，\[S_{\triangle OPQ}=8\left(\dfrac{4k^2+1}{1-4k^2}\right)=8\left(-1+\dfrac{2}{1-4k^2}\right);\]因为 $0\leqslant k^2<\dfrac 14$ 时，则 $0<1-4k^2\leqslant 1$，$\dfrac{2}{1-4k^2}\geqslant 2$，所以\[S_{\triangle OPQ}=8\left(-1+\dfrac{2}{1-4k^2}\right)\geqslant 8 ,\]当且仅当 $k=0$ 时取等号，所以当 $k=0$ 时，$S_{\triangle OPQ}$ 的最小值为 $8$．
综合（i）（ii）可知，当直线 $l$ 与椭圆 $C$ 在四个顶点处相切时，$\triangle OPQ$ 的面积取得最小值 $8$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
