如图，直三棱柱 $ ABC-A_1B_1C_1 $ 的底面是边长为 $ 2 $ 的正三角形，$ E $，$ F $ 分别是 $ BC $，$ CC_1 $ 的中点．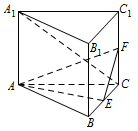
【难度】
【出处】
2015年高考湖南卷（文）
【标注】
-
证明：$ 平面AEF\perp 平面B_1BCC_1 $；标注答案略解析面面垂直一般通过线面垂直得到．因为三棱柱 $ ABC-A_1B_1C_1 $ 是直三棱柱，所以 $ AE\perp BB_1 $．
又 $ E $ 是正三角形 $ ABC $ 的边 $ BC $ 的中点，所以 $ AE\perp BC $．
又 $BB_1\cap BC=B$，因此 $ AE\perp 平面B_1BCC_1 $．
又 $ AE\subset 平面AEF $，所以 $ 平面AEF\perp 平面B_1BCC_1 $． -
若直线 $ A_1C $ 与平面 $ A_1ABB_1 $ 所成的角为 $ 45^\circ $，求三棱锥 $ F-AEC $ 的体积．标注答案$\dfrac{\sqrt 6}{12}$解析根据线面角定义将找出线面角对应的线线角是解决问题的关键．设 $ AB $ 的中点为 $ D $，连接 $ A_1D $，$ CD $，如图．
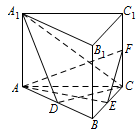因为 $ \triangle ABC $ 是正三角形，所以 $ CD\perp AB $．
又三棱柱 $ ABC-A_1B_1C_1 $ 是直三棱柱，所以 $ CD\perp AA_1 $．
又 $AB\cap AA_1=A$，因此 $ CD\perp 平面A_1ABB_1 $．
于是 $ \angle CA_1D $ 为直线 $ A_1C $ 与平面 $ A_1ABB_1 $ 所成的角．
由题设，$ \angle CA_1D=45^\circ $，所以 $ A_1D=CD=\dfrac{\sqrt 3}{2}AB=\sqrt 3 $．
在 ${\mathrm {Rt}}\triangle AA_1D$ 中，$ AA_1=\sqrt{A_1D^2-AD^2}=\sqrt{3-1}=\sqrt 2 $，所以 $ FC=\dfrac 12AA_1=\dfrac{\sqrt 2}{2} $．
故三棱锥 $ F-AEC $ 的体积$V=\dfrac 13S_{\triangle AEC}\cdot FC=\dfrac{1}{3}\times\dfrac{\sqrt 3}{2}\times \dfrac{\sqrt 2}{2}=\dfrac{\sqrt 6}{12}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
