已知抛物线 $ C_1:x^2=4y $ 的焦点 $ F $ 也是椭圆 $ C_2:\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1\left(a>b>0\right) $ 的一个焦点，$ C_1 $ 与 $ C_2 $ 的公共弦长为 $ 2\sqrt 6 $．过点 $F$ 的直线 $l$ 与 $C_1$ 相交于 $A$，$B$ 两点，与 $ C_2 $ 相交于 $ C $，$ D $ 两点，且 $ \overrightarrow{AC} $ 与 $ \overrightarrow{BD} $ 同向．
【难度】
【出处】
2015年高考湖南卷（文）
【标注】
-
求 $ C_2 $ 的方程；标注答案$\dfrac{y^2}{9}+\dfrac{x^2}{8}=1$解析由 $C_1:x^2=4y$ 知其焦点 $F$ 的坐标为 $\left(0,1\right)$．
因为 $F$ 也是椭圆 $C_2$ 的一个焦点，所以\[a^2-b^2=1. \quad \cdots \cdots ① \]又 $C_1$ 与 $C_2$ 的公共弦长为 $2\sqrt 6$，$C_1$ 关于 $y$ 轴对称，$C_2$ 关于 $y$ 轴对称且 $C_1$ 的方程为 $x^2=4y$，由此知 $C_1$ 与 $C_2$ 的公共点坐标为 $\left(\pm\sqrt 6,\dfrac{3}{2}\right)$，所以\[\dfrac{9}{4a^2}+\dfrac{6}{b^2}=1. \quad \cdots \cdots ② \]联立 $ ①② $ 得 $a^2=9$，$b^2=8$，故 $C_2$ 的方程为 $\dfrac{y^2}{9}+\dfrac{x^2}{8}=1$． -
若 $ \left|AC \right|= \left|BD \right| $，求直线 $l$ 的斜率．标注答案$\pm\dfrac{\sqrt 6}{4}$解析将共线的线段长度问题，转化为对应向量的横坐标的关系是解决问题的关键步骤．如图，设 $A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，$C\left(x_3,y_3\right)$，$D\left({x_4},{y_4}\right)$．
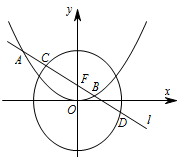因 $\overrightarrow{AC}$ 与 $\overrightarrow{BD}$ 同向，且 $ \left|AC \right|= \left|BD \right|$，所以 $\overrightarrow{AC}=\overrightarrow{BD}$，从而 $x_3-x_1=x_4-x_2$，即 $x_1-x_2=x_3-x_4$，于是\[\left(x_1+x_2\right)^2-4x_1x_2=\left(x_3+x_4\right)^2-4x_3x_4 . \quad \cdots \cdots ③ \]设直线 $l$ 的斜率为 $k$，则 $l$ 的方程为 $y=kx+1$．
联立直线与抛物线方程\[\begin{cases}
y=kx+1,\\
x^2=4y,\\
\end{cases}\]整理，得\[x^2-4kx-4=0.\]而 $x_1$，$x_2$ 是这个方程的两根，所以\[\begin{cases}x_1+x_2=4k, \\x_1x_2=-4. \end{cases}\quad \cdots \cdots ④ \]再联立直线与椭圆方程\[\begin{cases}y=kx+1,\\
\dfrac{y^2}{9}+\dfrac{x^2}{8}=1,\\
\end{cases}\]整理，得\[\left(9+8k^2\right)x^2+16kx-64=0,\]而 $x_3$，$x_4$ 是这个方程的两根，所以\[\begin{cases}x_3+{x_4}=-\dfrac{16k}{9+8k^2},\\x_1x_2=-\dfrac{64}{9+8k^2}.\end{cases} \quad \cdots \cdots ⑤ \]将 $ ④⑤ $ 代入 $ ③ $ 得\[16\left(k^2+1\right)=\dfrac{16^2k^2}{\left(9+8k^2\right)^2}+\dfrac{4\times 64}{9+8k^2},\]整理，得\[\left(9+8k^2\right)^2=16\times 9,\]解得 $k=\pm\dfrac{\sqrt 6}{4}$，即直线 $l$ 的斜率为 $\pm\dfrac{\sqrt 6}{4}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
