已知椭圆 $E$:$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1\left(a>b>0\right)$ 的半焦距为 $c$,原点 $O$ 到经过两点 $\left(c,0\right)$,$\left(0,b\right)$ 的直线的距离为 $\dfrac 12c$.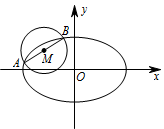

【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的离心率;标注答案$\dfrac {\sqrt 3}{2}$解析先求出经过点 $(c,0)$ 和 $(0,b)$ 的直线方程,然后利用点到直线的距离公式建立 $a,b,c$ 三者之间的关系,继而求出离心率.可求得过点 $\left(c,0\right)$,$\left(0,b\right)$ 的直线方程为\[bx+cy-bc=0,\]则原点 $O$ 到该直线的距离为 $\dfrac {bc}{\sqrt {b^2+c^2}}$.由题意,\[\dfrac {bc}{\sqrt {b^2+c^2}}=\dfrac 12c ,\]结合 $a^2=b^2+c^2$可得离心率为 $\dfrac ca=\dfrac {\sqrt 3}{2}$.
-
如图,$AB$ 是圆 $M$:$\left(x+2\right)^2+\left(y-1\right)^2=\dfrac 52$ 的一条直径,若椭圆 $E$ 经过 $A$,$B$ 两点,求椭圆 $E$ 的方程.标注答案$\dfrac {x^2}{12}+\dfrac {y^2}{3}=1$解析根据题意可得,$(-2,1)$ 为弦 $AB$ 的中点,且 $\left|AB\right|=\sqrt {10}$.设出 $AB$ 方程,与椭圆联立后利用弦长公式表达 $\left|AB\right|$,令 $\left|AB\right|=\sqrt {10}$,则可求出椭圆方程.方法一:
由(1)知,椭圆 $E$ 的方程为 $x^2+4y^2=4b^2. \quad \cdots \cdots ① $依题意,圆心 $M\left(-2,1\right)$ 是线段 $AB$ 的中点,且 $ \left|AB \right|=\sqrt {10}$.
易知,$AB$ 与 $x$ 轴不垂直,设其方程为 $y=k\left(x+2\right)+1$,直线 $AB$ 和椭圆 $E$ 的方程联立并消去 $y$ 得\[\left(1+4k^2\right)x^2+8k\left(2k+1\right)x+4\left(2k+1\right)^2-4b^2=0.\]设 $A\left(x_1,y_1\right)$,$B\left(x_2,y_2\right)$,则\[x_1+x_2=-\dfrac {8k\left(2k+1\right)}{1+4k^2} , x_1x_2= \dfrac {4\left(2k+1\right)^2-4b^2}{1+4k^2}.\]由因为 $M\left(-2,1\right)$ 是 $AB$ 中点,所以 $x_1+x_2=-4$,则\[-\dfrac {8k\left(2k+1\right)}{1+4k^2}=-4,\]解得 $k=\dfrac 12$.从而 $x_1x_2=8-2b^2$.于是根据弦长公式可得\[ \begin{split}\left|AB \right|&=\sqrt {1+\left(\dfrac 12\right)^2}\sqrt {\left(x_1+x_2\right)^2-4x_1x_2}\\&=\sqrt {10\left(b^2-2\right)}.\end{split}\]由 $ \left|AB \right|=\sqrt {10}$ 得\[\sqrt {10\left(b^2-2\right)}=\sqrt {10},\]解得 $b^2=3$.故椭圆 $E$ 的方程为 $\dfrac {x^2}{12}+\dfrac {y^2}{3}=1$.
方法二:
由(1)知,椭圆 $E$ 的方程为 $x^2+4y^2=4b^2. \quad \cdots \cdots ② $依题意,点 $A$,$B$ 关于圆心 $M\left(-2,1\right)$ 对称,且 $ \left|AB \right|=\sqrt {10}$.设 $A\left(x_1,y_1\right)$,$B\left(x_2,y_2\right)$,则\[x_1^2+4y_1^2=4b^2,x_2^2+4y_2^2=4b^2,\]两式相减并结合 $x_1+x_2=-4$,$y_1+y_2=2$得\[-4\left(x_1-x_2\right)+8\left(y_1-y_2\right)=0.\]易知 $AB$ 与 $x$ 轴不垂直,则 $x_1\neq x_2$,所以 $AB$ 的斜率$k_{AB}=\dfrac {y_1-y_2}{x_1-x_2}=\dfrac 12$.因此直线 $AB$ 的方程为\[y=\dfrac 12\left(x+2\right)+1.\]直线 $AB$ 的方程和椭圆 $E$ 的方程联立并消去 $y$ 得\[x^2+4x+8-2b^2=0.\]所以 $x_1+x_2=-4$,$x_1x_2=8-2b^2$.于是根据弦长公式可得\[ \begin{split}\left|AB \right|&=\sqrt {1+\left(\dfrac 12\right)^2}\sqrt {\left(x_1+x_2\right)^2-4x_1x_2}\\&=\sqrt {10\left(b^2-2\right)}.\end{split}\]由 $ \left|AB \right|=\sqrt {10}$,得\[\sqrt {10\left(b^2-2\right)}=\sqrt {10},\]解得 $b^2=3$.故椭圆 $E$ 的方程为 $\dfrac {x^2}{12}+\dfrac {y^2}{3}=1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2