如图，四棱锥 $P - ABCD$ 中，$AP \perp平面 PCD $，$ AD\parallel BC$，$AB = BC = \dfrac{1}{2}AD $，$E$，$F$ 分别为线段 $AD$，$PC$ 的中点．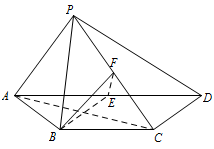
【难度】
【出处】
2014年高考山东卷（文）
【标注】
-
求证：$AP\parallel平面 BEF$；标注答案略解析此题考查线面平行，可以通过平行四边形和三角形的中位线作平面内一条直线与所证直线平行，或构造平面，通过面面平行证明即可．设 $AC$ 交 $BE$ 于点 $O$，连接 $OF$，$ EC $．
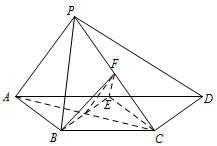不妨设 $AB = BC = 1$，则 $AD = 2$．
因为 $AB = BC$，$AD\parallel BC$，$ AE = BC $，所以四边形 $ABCE$ 为菱形．
又因为 $ O$，$F$ 分别为 $AC $，$ PC $ 中点，所以 $ OF\parallel AP$，
因为 $ OF \subset平面 BEF$，$AP \not\subset 平面 BEF $，所以 $ AP\parallel 平面 BEF$． -
求证：$BE \perp 平面 PAC$．标注答案略解析考查线面垂直．需要在平面 $PAC$ 内找到两条相交直线与 $BE$ 垂直．因为 $ AP \perp 平面 PCD$，$ CD \subset 平面 PCD $，所以 $ AP \perp CD$．
因为 $ BC\parallel ED$，$BC = ED$，所以四边形 $ BCDE$ 为平行四边形，
所以 $ BE\parallel CD$，所以 $ BE \perp PA$．
又因为四边形 $ ABCE$ 为菱形，所以 $ BE \perp AC$．
因为 $ PA \cap AC = A$，$ PA,AC \subset 平面 PAC $，所以 $ BE \perp 平面 PAC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
