如图1,四边形 $ABCD$ 为矩形,$PD \perp 面 ABCD$,$AB = 1$,$BC = PC = 2$,作如图2折叠,折痕 $EF \parallel DC$.其中点 $ E $,$ F $ 分别在线段 $ PD $,$ PC $ 上,沿 $EF$ 折叠后点 $P$ 叠在线段 $AD$ 上的点记为 $M$,并且 $MF \perp CF$.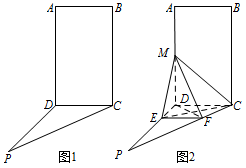

【难度】
【出处】
2014年高考广东卷(文)
【标注】
-
证明:$CF \perp 平面 MDF$;标注答案略解析本小题考查了线面垂直.难点是需要证一个线面垂直才能得到证明 $CF\perp$ 平面 $ADF$ 的条件.因为四边形 $ABCD$ 为矩形,所以 $MD \perp DC$,
因为 $PD \perp 平面 ABCD$,$MD \subset 平面 ABCD$,所以 $PD \perp MD$.
又 $PD \cap CD = D$,所以 $ MD \perp 平面 PCD$,
因为 $ CF \subset 平面 PCD$,所以 $ MD \perp CF$.
又 $ MF \perp CF $,$ MF \cap MD = M $,所以 $ CF \perp 平面 MDF$. -
求三棱锥 $M - CDE$ 的体积.标注答案$ V_{M-CDE}=\dfrac{\sqrt 2}{16}$.解析考查三棱锥的体积.因为 $ CF\perp 面 MDF $,$DF\subset 面 MDF$.
所以 $CF\perp DF $,所以在 ${\mathrm{Rt}} \triangle PCD $ 中,$ CD=1$,$PC=2 $,
所以 $\angle {PCD}= 60^ \circ$,且 $CD=1 $,
所以 $ CF=\dfrac{1}{2}$,故 $PF=\dfrac{3}{2} $,所以 $MF=\dfrac{3}{2} $.
又因为 $ CF\perp MF$,故由勾股定理得 $CM=\dfrac{\sqrt {10}}{2}$,
所以在 ${\mathrm {Rt}}\triangle MDC $ 中,$CM=\dfrac{\sqrt {10}}{2} $,$CD=1 $,得 $ DM=\dfrac{\sqrt{6}}{2}$.
又因为 $F $ 为 $ CP$(靠近 $ C $)的四等分点,故 $ PD=\sqrt 3$.
所以 $E $ 为 $PD $ 的四等分点,故 $ DE=\dfrac{\sqrt 3}{4}$.
所以 $S_{\triangle CDE} =\dfrac{1}{2}CD\cdot DE=\dfrac{1}{2}\times1\times\dfrac{\sqrt 3}{4}=\dfrac{\sqrt 3}{8}$.
所以 $ V_{M-CDE}=\dfrac{1}{3}S_{\triangle CDE}\cdot DM=\dfrac{\sqrt 2}{16}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2