查看数据源：599165c02bfec200011dfe21
已知 $\triangle ABP$ 的三个顶点都在抛物线 $C:{x^2} = 4y$ 上，$F$ 为抛物线 $C$ 的焦点，点 $M$ 为 $AB$ 的中点，$\overrightarrow {PF} = 3\overrightarrow {FM} $．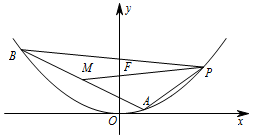
【难度】
【出处】
无
【标注】
  1. 若 $|PF| = 3$，求点 $M$ 的坐标；
    标注
    答案
    $M\left( - \dfrac{2\sqrt 2 }{3},\dfrac{2}{3}\right)$ 或 $ M\left(\dfrac{2\sqrt 2 }{3},\dfrac{2}{3}\right)$
    解析
    根据 $|PF|$ 可求出 $P$ 点的坐标，然后结合 $\overrightarrow {PF} = 3\overrightarrow {FM} $ 利用向量的坐标运算即可得到 $M$ 点的坐标．由题意知，焦点为 $F\left(0,1\right)$，准线方程为 $y = - 1$，设 $P\left({x_0},{y_0}\right)$，由抛物线的定义知，\[|PF| = {y_0} + 1,\]得到 ${y_0} = 2$，代入 ${x^2} = 4y$ 求得\[{x_0} = 2\sqrt 2 或 {x_0} = - 2\sqrt 2 ,\]所以 $P\left(2\sqrt 2 ,2\right)$ 或 $P\left( - 2\sqrt 2 ,2\right)$，由 $\overrightarrow {PF} = 3\overrightarrow {FM} $得\[M\left( - \dfrac{2\sqrt 2 }{3},\dfrac{2}{3}\right)或 M\left(\dfrac{2\sqrt 2 }{3},\dfrac{2}{3}\right).\]
  2. 求 $\triangle ABP$ 面积的最大值．
    标注
    答案
    $\dfrac{256\sqrt 5 }{135}$
    解析
    本题可以利用弦长公式和点到直线的距离公式表示三角形 $ABP$ 的面积，注意可以利用 $\overrightarrow {PF} = 3\overrightarrow {FM} $ 的关系转化为三角形 $ABF$ 的面积来求．设直线 $AB$ 的方程为 $y = kx + m$，$A\left({x_1},{y_1}\right)$，$B\left({x_2},{y_2}\right)$，$P\left({x_0},{y_0}\right)$，联立\[{\begin{cases}
    y = kx + m ,\\
    {x^2} = 4y, \\
    \end{cases}}\]得\[{x^2} - 4kx - 4m = 0,\]于是\[\Delta= 16{k^2} + 16m > 0,\]所以\[{x_1} + {x_2} = 4k,{x_1}{x_2} = - 4m,\]所以 $AB$ 的中点 $M$ 的坐标为 $\left(2k,2{k^2} + m\right)$，由 $\overrightarrow {PF} = 3\overrightarrow {FM} $，所以\[\left( - {x_0},1 - {y_0}\right) = 3\left(2k,2{k^2} + m - 1\right),\]所以\[{\begin{cases}{x_0} = - 6k ,\\
    {y_0} = 4 - 6{k^2} - 3m, \\
    \end{cases}}\]因为 $x_0^2 = 4{y_0}$，所以\[{k^2} =- \dfrac{1}{5}m + \dfrac{4}{15},\]由 $\Delta > 0$，$k^2 \geqslant 0$，得\[ - \dfrac{1}{3} < m \leqslant \dfrac{4}{3},\]由弦长公式可得\[|AB| = 4\sqrt {1 + {k^2}} \cdot \sqrt {{k^2} + m} ,\]点 $F\left(0,1\right)$ 到直线 $AB$ 的距离为 $\dfrac{|m - 1|}{{\sqrt {1 + {k^2}} }}$，所以\[\begin{split}{S_{\triangle ABP}} & = 4S{}_{\triangle ABF} \\& = 8|m - 1| \cdot \sqrt {{k^2} + m} \\& = \dfrac{16}{{\sqrt {15} }}\sqrt {3{m^3} - 5{m^2} + m+1} ,\end{split}\]记 $f\left(m\right) = 3{m^3} - 5{m^2} + m + 1$ $\left( - \dfrac{1}{3} < m \leqslant \dfrac{4}{3}\right)$，令\[f'\left(m\right) = 9{m^2} - 10m + 1 = 0,\]解得\[{m_1} = \dfrac{1}{9}, {m_2} = 1,\]所以 $f\left(m\right)$ 在 $\left( - \dfrac{1}{3},\dfrac{1}{9}\right)$ 上是增函数，在 $\left(\dfrac{1}{9},1\right)$ 上是减函数，在 $\left(1,\dfrac{4}{3}\right)$ 上是增函数，又\[f\left(\dfrac{1}{9}\right) = \dfrac{256}{243} > f\left(\dfrac{4}{3}\right),\]所以当 $m = \dfrac{1}{9}$ 时，$f\left(m\right)$ 取得最大值 $\dfrac{256}{243}$，此时 $k = \pm \dfrac{{\sqrt {55} }}{15}$，所以 $\triangle ABP$ 的面积的最大值为 $\dfrac{256\sqrt 5 }{135}$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.109723s