如图,设椭圆 $C:\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\left( {a > b > 0} \right)$,动直线 $l$ 与椭圆 $C$ 只有一个公共点 $P$,且点 $P$ 在第一象限.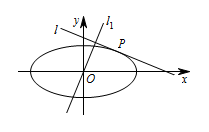

【难度】
【出处】
无
【标注】
-
已知直线 $l$ 的斜率为 $k$,用 $a$,$b$,$k$ 表示点 $P$ 的坐标;标注答案$ \left(\dfrac{{ - k{a^2}}}{{\sqrt {{a^2}{k^2} + {b^2}} }}, \dfrac{b^2}{{\sqrt {{a^2}{k^2} + {b^2}} }}\right)$.解析注意直线与圆相切的条件,联立直线与圆锥曲线后利用判别式等于零可解决.设直线方程为 $y = kx + m$ $\left(k<0\right)$,由\[\begin{cases}
\dfrac{x^2}{a^2} + \dfrac{y^2}{{{b^{^2}}}} = 1, \\
y = kx + m ,\\
\end{cases}\]消去 $y $,得\[\left(\dfrac{1}{a^2} + \dfrac{k^2}{b^2}\right){x^2} + \dfrac{2km}{b^2}x + \dfrac{m^2}{b^2} - 1 = 0,\]因为 $l $ 与 $ C$ 只有一个公共点 $P$,所以 $\Delta = 0$,得\[{m^2} = {b^2} + {a^2}{k^2}.\]此时方程的解为 $x=\dfrac{{ - k{a^2}}m}{{ {{a^2}{k^2} + {b^2}} }}$,即为点 $P$ 的横坐标,代入直线 $y=kx+m$,可得点 $P$ 的纵坐标为 $\dfrac{{b^2}m}{{ {{a^2}{k^2} + {b^2}} }}$,于是点 $ P$ 的坐标为\[\left(\dfrac{{ - k{a^2}}m}{{ {{a^2}{k^2} + {b^2}} }}, \dfrac{{b^2}m}{{ {{a^2}{k^2} + {b^2}} }}\right).\]又点 $P $ 在第一象限,故点 $P $ 的坐标为 $ \left(\dfrac{{ - k{a^2}}}{{\sqrt {{a^2}{k^2} + {b^2}} }}, \dfrac{b^2}{{\sqrt {{a^2}{k^2} + {b^2}} }}\right)$. -
若过原点 $O$ 的直线 ${l_1}$ 与 $l$ 垂直,证明:点 $P$ 到直线 ${l_1}$ 的距离的最大值为 $a - b$.标注答案略解析按点到直线的距离公式列出距离,然后注意变形后求最值即可.由于直线 $l_1 $ 过原点 $O $ 且与 $ l $ 垂直,故直线 $l_1 $ 的方程为 $x+ky=0 $,
设点 $ P$ 到直线 $l_1 $ 距离为 $ d$,则\[d=\dfrac{{\left|{\dfrac{-a^2k}{\sqrt{b^2+a^2k^2}}+\dfrac{b^2k}{\sqrt{b^2+a^2k^2}}}\right|}}{\sqrt{1+k^2}},\]整理得\[d=\dfrac{a^2-b^2}{\sqrt{b^2+a^2+a^2k^2+\dfrac{b^2}{k^2}}} .\]因为 $a^2k^2+\dfrac{b^2}{k^2} \geqslant 2ab$,所以\[\dfrac{a^2-b^2}{\sqrt{b^2+a^2+a^2k^2+\dfrac{b^2}{k^2}}}\leqslant \dfrac{a^2-b^2}{\sqrt{b^2+a^2+2ab}} =a-b,\]当且仅当 $ k^2=\dfrac{b}{a}$ 时等号成立.
所以点 $P $ 到直线 $ l_1$ 的距离的最大值为 $a-b $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2