当 $a \leqslant - 1$ 时，$M\left( a \right) - m\left( a \right) = 8$，
当 $ - 1 < a \leqslant \dfrac{1}{3}$ 时，$M\left( a \right) - m\left( a \right) = 4 - 3a - {a^3}$，
当 $\dfrac{1}{3} < a < 1$ 时，$M\left( a \right) - m\left( a \right) = 2 + 3a - {a^3}$，
当 $a \geqslant 1$ 时，$M\left( a \right) - m\left( a \right) = 4$．

本题需要对绝对值分类讨论，去掉绝对值后可利用导数求函数的最值．① 当 $a \leqslant - 1$ 时，$x - a \geqslant 0$，所以\[f\left( x \right) = {x^3} + 3x - 3a, f'\left( x \right) = 3{x^2} + 3 > 0,\]此时\[\begin{split}f{\left( x \right)_{\min }} & = m\left( a \right) = f\left( { - 1} \right) = - 1 - 3 - 3a = - 3a - 4 , \\ f{\left( x \right)_{\max }} & = M\left( a \right) = f\left( 1 \right) = 4 - 3a;\end{split}\]② 当 $ - 1 < a < 1$ 时，
1）当 $x \in \left( { - 1,a} \right)$ 时，$x - a < 0$，$ f\left( x \right) = {x^3} - 3x + 3a $，$ f'\left( x \right) = 3{x^2} - 3 < 0 $；
2）当 $x \in \left[ {a,1} \right)$ 时，$x - a \geqslant 0$，$ f\left( x \right) = {x^3} + 3x - 3a $，$ f'\left( x \right) = 3{x^2} + 3 > 0 $．
所以\[\begin{split}f{\left( x \right)_{\min }} & = m\left( a \right) = f\left( a \right) = {a^3} , \\ f{\left( x \right)_{\max }} & = M\left( a \right) = \max \left\{ {f\left( { - 1} \right),f\left( 1 \right)} \right\} = \max \left\{ {2 + 3a,4 - 3a} \right\},\end{split}\]由 $2 + 3a = 4 - 3a$，得 $a = \dfrac{1}{3}$，
所以当 $ - 1 < a \leqslant \dfrac{1}{3}$ 时，$M\left( a \right) = 4 - 3a$，当 $\dfrac{1}{3} < a < 1$ 时，$M\left( a \right) = 3a + 2$；
③ 当 $a \geqslant 1$ 时，$x - a \leqslant 0$，$f\left(x\right) = x^3-3x+3a$，$ f'\left( x \right) = 3{x^2} - 3 < 0 $，
此时\[\begin{split}f{\left( x \right)_{\min }} & = m\left( a \right) = f\left( 1 \right) = 3a - 2 , \\ f{\left( x \right)_{\max }} & = M\left( a \right) = f\left( { - 1} \right) = 3a + 2.\end{split}\]综上所述，
当 $a \leqslant - 1$ 时，$M\left( a \right) - m\left( a \right) = 8$，
当 $ - 1 < a \leqslant \dfrac{1}{3}$ 时，$M\left( a \right) - m\left( a \right) = 4 - 3a - {a^3}$，
当 $\dfrac{1}{3} < a < 1$ 时，$M\left( a \right) - m\left( a \right) = 2 + 3a - {a^3}$，
当 $a \geqslant 1$ 时，$M\left( a \right) - m\left( a \right) = 4$．

$ \left[ { - 2,0} \right] $

本题中两个变量 $a$、$b$ 无法转化为单变量，所以可以考虑用线性规划的思想来解决问题．由于 ${\left[ {f\left( x \right) + b} \right]^2} \leqslant 4$ 对于 $x \in \left[ { - 1,1} \right]$ 恒成立，即 $ - 2 - b \leqslant f\left( x \right) \leqslant 2 - b$ 对于 $x \in \left[ { - 1,1} \right]$ 恒成立，只需 $M\left( a \right) \leqslant 2 - b$，$m\left( a \right) \geqslant - 2 - b$ 即可．
① 当 $a \leqslant - 1$ 时，则\[ M\left( a \right) = 4 - 3a \leqslant 2 - b , m\left( a \right) = - 3a - 4 \geqslant - 2 - b, \]即 $3a + 2 \leqslant b \leqslant 3a - 2$，矛盾．
② 当 $ - 1 < a \leqslant \dfrac{1}{3}$ 时，则\[M\left( a \right) = 4 - 3a \leqslant 2 - b , m\left( a \right) = {a^3} \geqslant - 2 - b,\]即不等式组 $\begin{cases}
- 1 < a < \dfrac{1}{3} ,\\
3a - b - 2 \geqslant 0, \\
{a^3} + b + 2 \geqslant 0 \\
\end{cases}$ 成立，不等式组表示的平面区域如图所示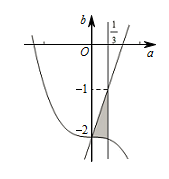．目标函数 $z = 3a + b$ 在 $\left( {0, - 2} \right)$ 取最小值 $ - 2$，在 $\left( {\dfrac{1}{3},0} \right)$ 取最大值 $0$．
③ 当 $\dfrac{1}{3} < a < 1$ 时，则\[M\left( a \right) = 3a + 2 \leqslant 2 - b , m\left( a \right) = {a^3} \geqslant - 2 - b,\]即不等式组 $\begin{cases}
\dfrac{1}{3} < a < 1, \\
3a + b \leqslant 0, \\
{a^3} + b + 2 \geqslant 0 \\
\end{cases}$ 成立，不等式组表示的平面区域如图所示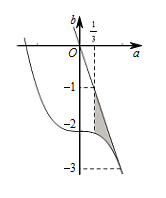．目标函数 $z = 3a + b$ 在 $\left( {\dfrac{1}{3}, - \dfrac{55}{27}} \right)$ 取最小值 $ - \dfrac{28}{27}$，在 $\left( {1, - 3} \right)$ 取最大值 $0$．
④ 当 $a \geqslant 1$ 时，则\[ M\left( a \right) = 3a + 2 \leqslant 2 - b , m\left( a \right) = 3a - 2 \geqslant - 2 - b, \]即 $3a + b \leqslant 0$ 且 $3a + b \geqslant 0$，则 $3a + b = 0$．
综上所述，若 ${\left[ {f\left( x \right) + b} \right]^2} \leqslant 4$ 对 $x \in \left[ { - 1,1} \right]$ 恒成立，则 $3a + b \in \left[ { - 2,0} \right] $．