如图，在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$E$、$F $、$P$、$Q$、$M$、$N$ 分别是棱 $AB$、$AD$、$D{D_1}$、$B{B_1}$、${A_1}{B_1}$、${A_1}{D_1}$ 的中点．求证：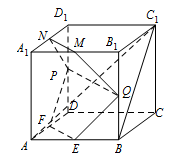
【难度】
【出处】
2014年高考湖北卷（文）
【标注】
-
直线 $B{C_1}\parallel $ 平面 $EFPQ$；标注答案略解析本题的关键是利用 $AD_1$ 过渡．如图所示，
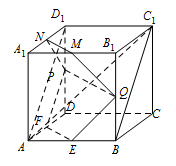连接 $ A{D_1} $，由 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 是正方体，知 $ A{D_1}\parallel B{C_1} $，
因为 $F、P$ 分别是 $AD、D{D_1}$ 的中点，所以 $ FP\parallel A{D_1} $．
从而 $ B{C_1}\parallel FP $．
而 $FP \subset $ 平面 $EFPQ$，且 $B{C_1} \not\subset $ 平面 $EFPQ$，
故直线 $B{C_1} \parallel $ 平面 $EFPQ$． -
直线 $A{C_1} \perp $ 平面 $PQMN$．标注答案略解析利用中位线转化为面对角线与体对角线的关系，可方便证明．如图所示，
连接 $AC,BD$，则 $AC \perp BD$．
由 $C{C_1} \perp $ 平面 $ABCD$，$BD \subset $ 平面 $ABCD$，可得 $C{C_1} \perp BD$．
又 $AC \cap C{C_1} = C$，所以 $BD \perp $ 平面 $AC{C_1}$．
而 $A{C_1} \subset $ 平面 $AC{C_1}$，所以 $BD \perp A{C_1}$．
因为 $ M、N $ 分别是 ${A_1}{B_1}、{A_1}{D_1}$ 的中点，所以 $ MN\parallel BD $，从而 $MN \perp A{C_1}$．
同理可证 $PN \perp A{C_1}$．
又 $PN \cap MN = N$，所以直线 $A{C_1}$ ⊥平面 $PQMN$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
