如图，四棱锥 $P - ABCD$ 中，$AB \perp AC$，$AB \perp PA$，$AB\parallel CD$，$AB = 2CD$，$E$、$F$、$G$、$M$、$N$ 分别为 $PB$、$AB$、$BC$、$PD$、$PC$ 的中点．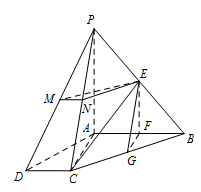
【难度】
【出处】
2013年高考山东卷（文）
【标注】
-
求证：$CE\parallel 平面 PAD$；标注答案略解析本题考查的是线面平行，线面平行的证明主要是通过构造中位线、平行四边形在平面内找到一条直线与已知直线平行即可，有时也可构造直线所在的平面与与已知平面平行，通过面面平行证明线面平行．如图，取 $PA$ 的中点 $H$，连接 $EH$，$DH$．
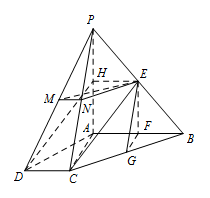因为 $E$ 为 $PB$ 的中点，所以 $EH\parallel AB$，$EH = \dfrac{1}{2}AB$．
又 $AB\parallel CD$，$CD = \dfrac{1}{2}AB$，所以 $EH\parallel CD$，$EH = CD$．
所以四边形 $DCEH$ 是平行四边形．所以 $CE\parallel DH$．
又 $DH \subset 平面 PAD$，$CE \not\subset 平面 PAD$，所以 $CE\parallel 平面 PAD$． -
求证：平面 $EFG \perp 平面 EMN$．标注答案略解析面面垂直一般是通过线面垂直来证明．因为 $E$，$F$ 分别为 $PB$，$AB$ 的中点，所以 $EF\parallel PA$．
又 $AB \perp PA$，所以 $AB \perp EF$，同理可证 $AB \perp FG$．
又 $EF \cap FG = F$，$EF \subset $ 平面 $EFG$，$FG \subset $ 平面 $EFG$，
因此 $AB \perp $ 平面 $EFG$．
又 $M$，$N$ 分别为 $PD$，$PC$ 的中点，所以 $MN\parallel DC$．
又 $AB\parallel DC$，所以 $MN\parallel AB$，所以 $MN \perp $ 平面 $EFG$．
又 $MN \subset $ 平面 $EMN$，所以平面 $EFG \perp $ 平面 $EMN$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
