如图 $(1)$,在边长为 $ 1 $ 的等边三角形 $ABC$ 中,$D$,$E$ 分别是 $AB$,$AC$ 边上的点,$AD = AE$,$F$ 是 $BC$ 的中点,$AF$ 与 $DE$ 交于点 $G$,将 $\triangle ABF$ 沿 $AF$ 折起,得到如图 $(2)$ 所示的三棱锥 $A - BCF$,其中 $BC = \dfrac{\sqrt 2 }{2}$.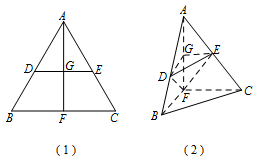

【难度】
【出处】
2013年高考广东卷(文)
【标注】
-
证明:$DE\parallel 平面 BCF$;标注答案略解析本小问关键是分析出折叠前后点线面的位置不变与变量,然后证明线面平行.在折叠后的图形中,因为 $AB = AC$,$AD = AE$,所以\[\dfrac{AD}{AB} = \dfrac{AE}{AC},\]故 $DE\parallel BC$.
因为 $DE \not\subset 平面BCF$,$BC \subset 平面 BCF$,所以 $DE\parallel 平面 BCF$. -
证明:$CF \perp 平面 ABF$;标注答案略解析本小问与第 $(1)$ 问相似,需要先分析折叠前后的变量与不变量,然后证明线面垂直.在折叠前的图形中,因为 $\triangle ABC$ 为等边三角形,$BF = CF$,所以 $AF \perp BC$,则在折叠后的图形中,$AF \perp BF$,$AF \perp CF$.又\[BF = CF = \dfrac{1}{2},BC = \dfrac{\sqrt 2 }{2},\]所以\[B{C^2} = B{F^2} + C{F^2},\]所以 $BF \perp CF$.又 $BF \cap AF = F$,$BF \subset $ 平面 $ABF$,$AF \subset $ 平面 $ABF$,所以 $CF \perp $ 平面 $ABF$.
-
当 $AD = \dfrac{2}{3}$ 时,求三棱锥 $F - DEG$ 的体积 ${V_{F - DEG}}$.标注答案三棱锥 $F - DEG$ 的体积为 $ \dfrac{\sqrt 3 }{324} $解析本小问考查三棱锥的体积.由 $(1)$ 可知 $DG\parallel BF$,$GE\parallel FC$,又 $AF\perp BF$,所以 $DG\perp AF$.由 $(2)$ 知,$CF \perp $ 平面 $ABF$,于是 $GE\perp 平面ABF$.在折叠前的图形中,\[AB = 1,BF = CF = \dfrac{1}{2},AF = \dfrac{\sqrt 3 }{2}.\]所以\[DG=GE=\dfrac{2}{3},GF=\dfrac{1}{3}AF=\dfrac{\sqrt 3}{6},\]故三棱锥 $A-BCF$ 的体积为\[\begin{split}V_{A-BCF}&=\dfrac{1}{3}S_{\triangle DGF}\cdot GE\\&=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot DG\cdot GF\cdot GE\\&=\dfrac{\sqrt 3}{243}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3