如图，$AB $ 是圆 $O $ 的直径，$PA $ 垂直圆 $O $ 所在的平面，$ C$ 是圆 $ O$ 上的点．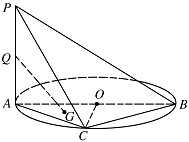
【难度】
【出处】
2013年高考辽宁卷（文）
【标注】
-
求证：$BC\perp $ 平面 $PAC $；标注答案略解析在面上找两条相交直线均垂直于 $BC$ 即可．由 $ AB $ 是圆 $ O $ 的直径，得 $ AC \perp BC $，
由 $ PA \perp $ 平面 $ ABC $，$ BC \subset $ 平面 $ ABC $，得 $ PA \perp BC $．又 $ PA \cap AC = A $，$ PA \subset $ 平面 $ PAC $，$ AC \subset $ 平面 $ PAC $，
所以 $ BC \perp $ 平面 $ PAC $． -
设 $Q $ 为 $PA $ 的中点，$G $ 为 $ \triangle AOC$ 的重心，求证：$ QG\parallel $ 平面 $ PBC $．标注答案略解析线面平行常有两种处理方式：① 在面上找一条直线平行于已知直线；② 利用面面平行的性质，若两面平行，则其中一面上的任意直线平行于另一平面．连接 $ OG $ 并延长交 $ AC $ 于点 $ M $，连接 $ QM,QO $，
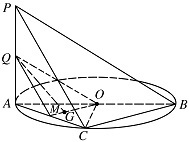由 $ G $ 为 $ \triangle AOC $ 的重心，得 $ M $ 为 $ AC $ 中点．
由 $ Q $ 为 $ PA $ 中点，得 $ QM\parallel PC $，又 $ O $ 为 $ AB $ 中点，得 $ OM\parallel BC $．
因为 $ QM \cap MO = M $，$ QM \subset $ 平面 $ QMO $，$ MO \subset $ 平面 $ QMO $，$ BC \cap PC = C $，$ BC \subset $ 平面 $ PBC $，$ PC \subset $ 平面 $ PBC $，所以平面 $ QMO\parallel $ 平面 $ PBC $．
又因为 $ QG \subset $ 平面 $ QMO $，所以 $ QG\parallel $ 平面 $ PBC $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
