如图,四棱锥 $P - ABCD$ 中,$PA \perp $ 底面 $ABCD$,$PA = 2\sqrt 3 $,$BC = CD = 2$,$\angle ACB = \angle ACD = \dfrac{\mathrm \pi} {3}$.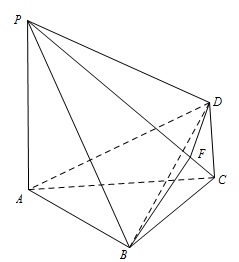

【难度】
【出处】
2013年高考重庆卷(文)
【标注】
-
求证:$BD \perp $ 平面 $PAC$;标注答案略解析本题可证明 $BD$ 与 $AC$ 和 $PA$ 垂直.$PA$ 和 $BD$ 的垂直可利用线面垂直的性质定理证明,$AC$ 和 $BD$ 垂直可利用四边形 $ABCD$ 中的边角关系来证明.因为 $BC = CD$,所以 $\triangle BCD$ 为等腰三角形.
又 $\angle ACB = \angle ACD$,所以 $BD \perp AC$.
因为 $PA \perp $ 底面 $ABCD$,所以 $PA \perp BD$.
从而 $BD$ 与平面 $PAC$ 内两条相交直线 $PA,AC$ 都垂直,
所以 $BD \perp $ 平面 $PAC$. -
若侧棱 $PC$ 上的点 $F$ 满足 $PF = 7FC$,求三棱锥 $P - BDF$ 的体积.标注答案$\dfrac{7}{4}$解析三棱锥 $P-BDF$ 的体积可以用 $P-BCD$ 的体积减去 $F-BCD$ 的体积来计算.三棱锥 $P - BCD$ 的底面 $BCD$ 的面积为\[\begin{split}{S_{\triangle BCD}} &= \dfrac{1}{2}BC \cdot CD \cdot \sin \angle BCD\\&= \dfrac{1}{2} \times 2 \times 2 \times \sin \dfrac{{2{\mathrm \pi} }}{3} \\&= \sqrt 3. \end{split}\]由 $PA \perp $ 底面 $ABCD$,得三棱锥 $P-BCD$ 的体积为\[\begin{split}{V_{P - BCD}} &= \dfrac{1}{3} \cdot {S_{\triangle BCD}} \cdot PA \\&= \dfrac{1}{3} \times \sqrt 3 \times 2\sqrt 3 \\&= 2.\end{split}\]由 $PF = 7FC$,得三棱锥 $F - BCD$ 的高为 $\dfrac{1}{8}PA$,所以它的体积为\[\begin{split}{V_{F - BCD}} &= \dfrac{1}{3} \cdot {S_{\triangle BCD}} \cdot \dfrac{1}{8}PA \\&= \dfrac{1}{3} \times \sqrt 3 \times \dfrac{1}{8} \times 2\sqrt 3 \\&= \dfrac{1}{4},\end{split}\]所以\[\begin{split}{V_{P - BDF}} &= {V_{P - BCD}} - {V_{F - BCD}} \\&= 2 - \dfrac{1}{4} \\&= \dfrac{7}{4}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2