如图,椭圆的中心为原点 $O$,长轴在 $x$ 轴上,离心率 $e = \dfrac{\sqrt 2 }{2}$,过左焦点 ${F_1}$ 作 $x$ 轴的垂线交椭圆于 $A$,$A'$ 两点,$\left| {AA'} \right| = 4$.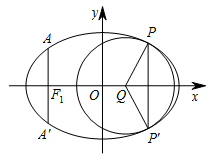

【难度】
【出处】
2013年高考重庆卷(文)
【标注】
-
求该椭圆的标准方程;标注答案$\dfrac{x^2}{16} + \dfrac{y^2}{8} = 1$解析本题考查椭圆的标准方程相关知识.根据题意,$\left|AA_1\right|$ 为椭圆的通径,所以 $\dfrac {2b^2}a=4\cdots\cdots ① $,又离心率$\mathrm e=\dfrac ca=\dfrac {\sqrt 2}2\cdots\cdots ② $,由 ①② 并结合 $a^2=b^2+c^2$得 $a=4,b=2\sqrt 2$,所以椭圆的标准方程为\[\dfrac{x^2}{16} + \dfrac{y^2}{8} = 1.\]
-
取平行于 $y$ 轴的直线与椭圆相交于不同的两点 $P$,$P'$,过 $P$,$P'$ 作圆心为 $Q$ 的圆,使椭圆上的其余点均在圆 $Q$ 外,求 $\triangle PP'Q$ 的面积 $S$ 的最大值,并写出对应的圆 $Q$ 的标准方程.标注答案这样的圆有两个,其标准方程分别为\[\begin{split}{\left( {x + \sqrt 2 } \right)^2} + {y^2} &= 6 , \\ {\left( {x - \sqrt 2 } \right)^2} + {y^2} &= 6.\end{split}\]解析本题解决关键在于椭圆上的点到圆心的距离最短的转化,求解出三角形面积表达式.由椭圆的对称性,可设 $Q\left({x_0},0\right)$.又设 $M\left(x,y\right)$ 是椭圆上任意一点,则 $\dfrac {x^2}{16}+\dfrac {y^2}8=1$,根据两点间距离公式有\[\begin{split} \left|QM \right|^2 &= {\left(x - {x_0}\right)^2} + {y^2} \\&= {x^2} - 2{x_0}x + x_0^2 + 8\left( {1 - \dfrac{x^2}{16}} \right) \\&= \dfrac{1}{2}{\left(x - 2{x_0}\right)^2} - x_0^2 + 8\left(x \in \left[ - 4,4\right] \right).\end{split}\]设 $P\left({x_1},{y_1}\right)$,由题意知,点 $P$ 是椭圆上到点 $Q$ 的距离最小的点,
因此,上式当 $x = {x_1}$ 时取最小值.又因为 ${x_1} \in \left( - 4,4\right)$,
所以,上式当 $x = 2{x_0}$ 时取最小值,从而 ${x_1} = 2{x_0}$,$ \left|QP \right|^2 = 8 - x_0^2$.
由对称性知 $P' \left({x_1},- {y_1} \right)$,故 $ \left|PP'\right| = \left|2{y_1}\right|$,所以\[\begin{split}S &= \dfrac{1}{2} \left|2{y_1} \right| \cdot \left|{x_1} - {x_0} \right| \\&= \dfrac{1}{2} \cdot 2\sqrt {8\left( {1 - \dfrac{x_1^2}{16}} \right)} \cdot \left|{x_0}\right| \\&= \sqrt 2 \cdot \sqrt { \left(4 - x_0^2 \right)x_0^2} \\&= \sqrt 2 \cdot \sqrt { - {{ \left(x_0^2 - 2 \right)}^2} + 4}.\end{split}\]当 ${x_0} = \pm \sqrt 2 $ 时,$\triangle PP'Q$ 的面积 $S$ 取到最大值$2\sqrt 2 $.此时对应的圆 $Q$ 的圆心坐标为 $Q \left( \pm \sqrt 2,0 \right)$,半径\[ \left|QP \right| = \sqrt {8 - x_0^2} = \sqrt 6, \]因此,这样的圆有两个,其标准方程分别为\[\begin{split}{\left( {x + \sqrt 2 } \right)^2} + {y^2} &= 6 , \\ {\left( {x - \sqrt 2 } \right)^2} + {y^2} &= 6.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2