如图,四棱锥 $P - ABCD$ 中,$PA \perp $ 底面 $ABCD$,$BC = CD = 2$,$AC = 4$,$\angle ACB = \angle ACD = \dfrac{\mathrm \pi} {3}$,$F$ 为 $PC$ 的中点,$AF \perp PB$.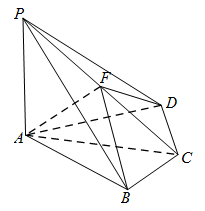

【难度】
【出处】
无
【标注】
-
求 $PA$ 的长;标注答案$ 2\sqrt{3} $.解析本题可以建立适当的坐标系,利用空间向量计算线段长度.如图,连接 $ BD $ 交 $ AC $ 于点 $ O $,因为 $ BC=CD $,即 $ \triangle BCD $ 为等腰三角形,
又 $ AC $ 平分 $ \angle BCD $,故 $ AC\perp BD $.接下来可用空间向量表达 $AF$ 和 $PB$ 的垂直关系.
以 $ O $ 为坐标原点,$ \overrightarrow{OB},\overrightarrow{OC},\overrightarrow{AP} $ 的方向分别为 $ x $ 轴,$ y $ 轴,$ z $ 轴的正方向,建立空间直角坐标系 $ O-xyz $,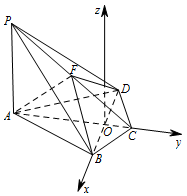 则\[ OC=CD\cos \dfrac{\mathrm \pi} {3}=1 .\]而 $ AC=4 $,所以 $ AO=AC-OC=3 $.又\[ OD=CD\sin \dfrac{\mathrm \pi} {3}=\sqrt{3} ,\]故\[A\left( 0,-3,0 \right),B\left( \sqrt{3},0,0 \right),C\left( 0,1,0 \right),D\left( -\sqrt{3},0,0 \right).\]因为 $ PA\perp $ 底面 $ ABCD $,可设 $ P\left( 0,-3,z \right) $,由点 $ F $ 为 $ PC $ 边中点,$ F\left( 0,-1,\dfrac{z}{2} \right) $.又\[\begin{split} \overrightarrow{AF} &=\left( 0,2,\dfrac{z}{2} \right),\\ \overrightarrow{PB} &=\left( \sqrt{3},3,-z \right), \end{split}\]因为 $ AF\perp PB $,故\[ \overrightarrow{AF}\cdot \overrightarrow{PB}=0, \]即 $ 6-\dfrac{{{z}^{2}}}{2}=0,z=2\sqrt{3} $($ z=-2\sqrt{3} $ 舍去),所以\[ \left|\overrightarrow{PA} \right|=2\sqrt{3}, \]所以 $ PA $ 的长为 $ 2\sqrt{3} $.
则\[ OC=CD\cos \dfrac{\mathrm \pi} {3}=1 .\]而 $ AC=4 $,所以 $ AO=AC-OC=3 $.又\[ OD=CD\sin \dfrac{\mathrm \pi} {3}=\sqrt{3} ,\]故\[A\left( 0,-3,0 \right),B\left( \sqrt{3},0,0 \right),C\left( 0,1,0 \right),D\left( -\sqrt{3},0,0 \right).\]因为 $ PA\perp $ 底面 $ ABCD $,可设 $ P\left( 0,-3,z \right) $,由点 $ F $ 为 $ PC $ 边中点,$ F\left( 0,-1,\dfrac{z}{2} \right) $.又\[\begin{split} \overrightarrow{AF} &=\left( 0,2,\dfrac{z}{2} \right),\\ \overrightarrow{PB} &=\left( \sqrt{3},3,-z \right), \end{split}\]因为 $ AF\perp PB $,故\[ \overrightarrow{AF}\cdot \overrightarrow{PB}=0, \]即 $ 6-\dfrac{{{z}^{2}}}{2}=0,z=2\sqrt{3} $($ z=-2\sqrt{3} $ 舍去),所以\[ \left|\overrightarrow{PA} \right|=2\sqrt{3}, \]所以 $ PA $ 的长为 $ 2\sqrt{3} $. -
求二面角 $B - AF - D$ 的正弦值.标注答案$ \dfrac{3\sqrt{7}}{8} $.解析本题考查空间向量计算二面角的相关知识.可用向量法求二面角 $B-AF-D$ 的大小.
由(1)知,\[\begin{split} \overrightarrow{AD} &=\left( -\sqrt{3},3,0 \right),\\ \overrightarrow{AB} &=\left( \sqrt{3},3,0 \right),\\ \overrightarrow{AF} &=\left( 0,2,\sqrt{3} \right) .\end{split}\]设平面 $ FAD $ 的法向量为 $ \overrightarrow{{{n}_{1}}}=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) $,平面 $ FAB $ 的法向量为 $ \overrightarrow{{{n}_{2}}}=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) $,由\[\begin{cases} \overrightarrow{{{n}_{1}}}\cdot \overrightarrow{AD}&=0,\\ \overrightarrow{{{n}_{1}}}\cdot \overrightarrow{AF} &=0, \end{cases}\]得\[ \begin{cases}& -\sqrt{3}{{x}_{1}}+3{{y}_{1}}=0, \\
& 2{{y}_{1}}+\sqrt{3}{{z}_{1}}=0, \\
\end{cases} \]因此可取\[ \overrightarrow{{{n}_{1}}}=\left( 3,\sqrt{3},-2 \right) .\]由\[\begin{cases} \overrightarrow{{{n}_{2}}}\cdot \overrightarrow{AB} &=0,\\ \overrightarrow{{{n}_{2}}}\cdot \overrightarrow{AF} &=0, \end{cases}\]得\[ \begin{cases}& \sqrt{3}{{x}_{2}}+3{{y}_{2}}=0, \\
& 2{{y}_{2}}+\sqrt{3}{{z}_{2}}=0, \\
\end{cases}\]故可取\[ \overrightarrow{{{n}_{2}}}=\left( 3,-\sqrt{3},2 \right). \]从而法向量 $ \overrightarrow{{{n}_{1}}}$,$\overrightarrow{{{n}_{2}}} $ 的夹角的余弦值为\[\begin{split}\cos \langle \overrightarrow{{{n}_{1}}},\overrightarrow{{{n}_{2}}} \rangle &=\frac{\overrightarrow{{{n}_{1}}}\cdot \overrightarrow{{{n}_{2}}}}{ \left|\overrightarrow{{{n}_{1}}} \right|\cdot \left|\overrightarrow{{{n}_{2}}} \right|}=\frac{1}{8},\end{split}\]故二面角 $ B-AF-D $ 的正弦值为 $ \dfrac{3\sqrt{7}}{8} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2