下图是某市 $ 3 $ 月 $ 1 $ 日至 $ 14 $ 日的空气质量指数趋势图,空气质量指数小于 $ 100 $ 表示空气质量优良,空气质量指数大于 $ 200 $ 表示空气重度污染.某人随机选择 $ 3 $ 月 $ 1 $ 日至 $ 3 $ 月 $ 13 $ 日中的某一天到达该市,并停留 $ 2 $ 天.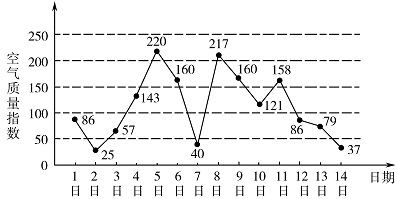

【难度】
【出处】
2013年高考北京卷(文)
【标注】
-
求此人到达当日空气质量优良的概率;标注答案$\dfrac{6}{13}$解析本题考查古典概型.在 $ 3 $ 月 $ 1 $ 日至 $ 3 $ 月 $ 13 $ 日这 $ 13 $ 天中,$ 1 $ 日、$ 2 $ 日、$ 3 $ 日、$ 7 $ 日、$ 12 $ 日、$ 13 $ 日共 $ 6 $ 天的空气质量优良,所以此人到达当日空气质量优良的概率是\[P=\dfrac{6}{13}.\]
-
求此人在该市停留期间只有 $ 1 $ 天空气质量重度污染的概率;标注答案$\dfrac{4}{13}$解析本题考查古典概型.根据题意,事件"此人在该市停留期间只有 $ 1 $ 天空气质量重度污染"等价于"此人到达该市的日期是 $ 4 $ 日,或 $ 5 $ 日,或 $ 7 $ 日,或 $ 8 $ 日",所以此人在该市停留期间只有 $ 1 $ 天空气质量重度污染的概率为\[P=\dfrac{4}{13}.\]
-
由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)标注答案从 $ 3 $ 月 $ 5 $ 日开始连续三天的空气质量指数方差
样本的数字特征 最大解析波动越大方差越大.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3