如图,在四棱锥 $P - ABCD$ 中,$AB\parallel CD$,$AB \perp AD$,$CD = 2AB$,平面 $PAD \perp 底面 ABCD$,$PA \perp AD$,$E$ 和 $F$ 分别是 $CD$ 和 $PC$ 的中点.求证: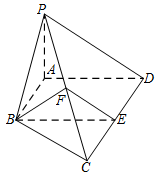

【难度】
【出处】
2013年高考北京卷(文)
【标注】
-
$PA \perp 底面 ABCD$;标注答案略解析在面中找两条相交直线均垂直于直线 $PA$ 即可.因为平面 $PAD \perp$ 底面 $ABCD$,且平面 $PAD \cap $ 底面 $ ABCD=AD$,$PA\subset $ 平面 $PAD$,$PA\perp AD$,
所以 $PA \perp 底面 ABCD$. -
$BE\parallel 平面 PAD$;标注答案略解析在面上找一条直线平行于 $BE$ 即可.因为 $AB\parallel CD$,$CD = 2AB$,$E$ 为 $CD$ 的中点,所以 $AB\parallel DE$,且 $AB = DE$.
所以四边形 $ABED$ 为平行四边形.所以 $BE\parallel AD$.
又因为 $BE \not\subset $ 平面 $ PAD$,$AD \subset $ 平面 $ PAD$,
所以 $BE \parallel 平面 PAD$. -
平面 $BEF \perp 平面 PCD$.标注答案略解析线垂直于面,则过该直线的平面均垂直于已知平面.因为 $AB \perp AD$,而且四边形 $ABED$ 为平行四边形,所以 $BE \perp CD$,$AD \perp CD$.
由 $(1)$ 知 $PA \perp 底面 ABCD$,所以 $PA \perp CD$.又因为 $ PA\cap AD=A $,
所以 $CD \perp $ 平面 $ PAD$.所以 $CD \perp PD$.
因为 $E$ 和 $F$ 分别是 $CD$ 和 $PC$ 的中点,
所以 $PD\parallel EF$.所以 $CD \perp EF$.
又因为 $CD \perp BE$,$EF \cap BE = E$,所以 $CD \perp 平面 BEF$.
所以平面 $BEF \perp 平面 PCD$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3