如图，四棱锥 $P - ABCD$ 中，$\angle ABC = \angle BAD = 90^\circ $，$BC = 2AD$，$\triangle PAB$ 和 $\triangle PAD$ 都是边长为 $ 2 $ 的等边三角形．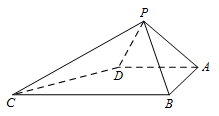
【难度】
【出处】
2013年高考大纲卷（文）
【标注】
-
证明：$PB \perp CD$；标注答案略解析题中的异面直线不容易移动成为共面直线，可以考虑利用线面垂直的性质（线垂直于面则垂直于面内所有直线）证明线线垂直．取 $BC$ 的中点 $E$，连接 $DE$，则四边形 $ABED$ 为正方形．
过点 $P$ 作 $PO \perp 平面 ABCD$，垂足为 $O$．
连接 $OA$，$OB$，$OD$，$OE$．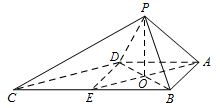
由 $\triangle PAB$ 和 $\triangle PAD$ 都是等边三角形，知 $PA = PB = PD$，
所以 $OA = OB = OD$，即点 $O$ 为正方形 $ABED$ 对角线的交点，
故 $OE \perp BD$，从而 $PB \perp OE$．
因为 $O$ 是 $BD$ 的中点，$E$ 是 $BC$ 的中点，
所以 $OE\parallel CD$．因此 $PB \perp CD$． -
求点 $A$ 到平面 $PCD$ 的距离．标注答案$ 1 $解析考虑到点 $A$ 到平面的垂线不好找，可根据平行于平面的直线上的点到平面的距离均相等，将点 $A$ 到平面 $PCD$ 的距离，转化为点 $O$ 到平面 $PCD$ 的距离．取 $PD$ 的中点 $F$，连接 $OF$，则 $OF\parallel PB$．
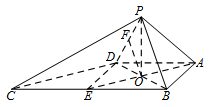由 $(1)$ 知，$PB \perp CD$，故 $OF \perp CD$．又\[ \begin{split}OD &= \dfrac{1}{2}BD = \sqrt 2, \\ OP &= \sqrt {P{D^2} - O{D^2}} = \sqrt 2 ,\end{split} \]故 $\triangle POD$ 为等腰三角形，因此 $OF \perp PD$．
又 $PD \cap CD = D$，
所以 $OF \perp 平面 PCD$．
因为 $AE\parallel CD$，$CD \subset 平面 PCD$，$AE \not\subset 平面 PCD$，
所以 $AE\parallel 平面 PCD$．
因此点 $O$ 到平面 $PCD$ 的距离 $OF$ 就是点 $A$ 到平面 $PCD$ 的距离，而\[OF = \dfrac{1}{2}PB = 1,\]所以点 $A$ 到平面 $PCD$ 的距离为 $ 1 $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
