如图,在三棱锥 $V-ABC$ 中,$平面VAB\perp 平面ABC$,$\triangle VAB$ 为等边三角形,$AC\perp BC$ 且 $AC=BC=\sqrt2$,$O$,$M$ 分别为 $AB$,$VA$ 的中点.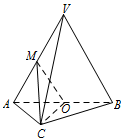

【难度】
【出处】
2015年高考北京卷(文)
【标注】
-
求证:$VB\parallel 平面MOC$;标注答案略解析根据线面平行的判定定理,找出面 $MOC$ 上与直线 $VB$ 平行的直线即可.因为 $O$,$M$ 分别为 $AB$,$VA$ 的中点,
所以 $OM\parallel VB$.
又因为 $VB\not\subset 平面MOC$,$ OM\subset 平面 MOC $,
所以 $VB\parallel 平面MOC$. -
求证:$平面MOC\perp 平面VAB$;标注答案略解析根据面面垂直的判定定理,找出其中一个面上垂直另一个面的直线即可.因为 $AC=BC$,$O$ 为 $AB$ 的中点,
所以 $OC\perp AB$.
又因为 $平面VAB\perp 平面ABC$,交线为 $AB$,且 $OC\subset 平面ABC$,
所以 $OC\perp 平面VAB$.
所以 $平面MOC\perp 平面VAB$. -
求三棱锥 $V-ABC$ 的体积.标注答案$\dfrac{\sqrt3}{3}$解析本题考查三棱锥的体积计算.选择合适的顶点是求解三棱锥体积的关键.在等腰直角三角形 $ACB$ 中,因为 $AC=BC=\sqrt2$,
所以 $AB=2$,$OC=1$.
所以等边三角形 $VAB$ 的面积 $S_{\triangle VAB} =\sqrt3$.
又因为 $OC\perp 平面VAB$,
所以 $OC$ 为三棱锥 $C-VAB$ 的高,
所以三棱锥 $C-VAB$ 的体积等于 $\dfrac13OC\cdot S_{\triangle VAB}=\dfrac{\sqrt3}{3}$.
又因为三棱锥 $V-ABC$ 的体积与三棱锥 $C-VAB$ 的体积相等,
所以三棱锥 $V-ABC$ 的体积为 $\dfrac{\sqrt3}{3}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3