某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为 $l_1$,$l_2$,山区边界曲线为 $C$,计划修建的公路为 $l$.如图所示,$M$,$N$ 为 $C$ 的两个端点,测得点 $M$ 到 $l_1$,$l_2$ 的距离分别为 $5$ 千米和 $40$ 千米,点 $N$ 到 $l_1$,$l_2$ 的距离分别为 $20$ 千米和 $2.5$ 千米.以 $l_2$,$l_1$ 所在的直线分别为 $x$,$y$ 轴,建立平面直角坐标系 $xOy$.假设曲线 $C$ 符合函数 $y=\dfrac{a}{x^2+b}$(其中 $a$,$b$ 为常数)模型.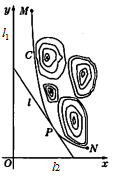

【难度】
【出处】
2015年高考江苏卷
【标注】
-
求 $a$,$b$ 的值;标注答案$\begin{cases}
a=1000,\\
b=0.
\end{cases}$解析将点 $M(5,40)$ 和点 $N(20,2.5)$ 的坐标代入函数 $y=\dfrac{a}{x^2+b}$ 的解析式中即可求出 $a,b$.由题意知,点 $M$,$N$ 的坐标分别为 $\left(5,40\right)$,$\left(20,2.5\right)$.
将其分别代入 $y=\dfrac{a}{x^2+b}$,得 $\begin{cases}
\dfrac{a}{25+b}=40,\\
\dfrac{a}{400+b}=2.5,
\end{cases}$解得 $\begin{cases}a=1000,\\
b=0.
\end{cases}$ -
设公路 $l$ 与曲线 $C$ 相切于 $P$ 点,$P$ 的横坐标为 $t$.
(i)请写出公路 $l$ 长度的函数解析式 $f\left(t\right)$,并写出其定义域;
(ii)当 $t$ 为何值时,公路 $l$ 的长度最短?求出最短长度.标注答案(i)$f\left(t\right)=\sqrt{\left(\dfrac{3t}2\right)^2+\left(\dfrac{3 000}{t^2}\right)^2}
=\dfrac 32\sqrt{t^2+\dfrac{4\times 10^6}{t^4}}$,$t\in\left[5,20\right]$.
(ii)当 $t=10\sqrt 2$ 时,公路 $l$ 的长度最短,最短长度为 $15\sqrt 3$ 千米解析先求出直线 $l$ 的方程,然后利用两点间距离公式建立 $f(t)$ 的表达式,最后利用导数求 $f(t)$ 最小值即可.(i)由 $(1)$ 知,$y=\dfrac{1000}{x^2}\left(5\leqslant x\leqslant 20\right)$,则点 $P$ 的坐标为 $\left(t,\dfrac{1000}{t^2}\right)$.
设在点 $P$ 处的切线 $l$ 交 $x$,$y$ 轴分别于 $A$,$B$ 两点.$y'=-\dfrac{2 000}{x^3}$,则 $l$ 的方程为 $y-\dfrac{1 000}{t^2}=-\dfrac{2 000}{t^3}\left(x-t\right)$,
由此得 $A\left(\dfrac{3t}2,0\right)$,$B\left(0,\dfrac{3 000}{t^2}\right)$.
故 $f\left(t\right)=\sqrt{\left(\dfrac{3t}2\right)^2+\left(\dfrac{3 000}{t^2}\right)^2}
=\dfrac 32\sqrt{t^2+\dfrac{4\times 10^6}{t^4}}$,$t\in\left[5,20\right]$.
(ii)设 $g\left(t\right)=t^2+\dfrac{4\times 10^6}{t^4}$,则 $g'\left(t\right)=2t-\dfrac{16\times 10^6}{t^5}$.
令 $g'\left(t\right)=0$,解得 $t=10\sqrt 2$.
当 $t\in\left(5,10\sqrt 2\right)$ 时,$g'\left(t\right)<0$,$g\left(t\right)$ 是减函数;
当 $t\in\left(10\sqrt 2,20\right)$ 时,$g'\left(t\right)>0$,$g\left(t\right)$ 是增函数.
从而,当 $t=10\sqrt 2$ 时,函数 $g\left(t\right)$ 有极小值,也是最小值,
所以 $g\left(t\right)_{\min}=300$,此时 $f\left(t\right)_{\min}=15\sqrt 3$.
答:当 $t=10\sqrt 2$ 时,公路 $l$ 的长度最短,最短长度为 $15\sqrt 3$ 千米.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2