查看数据源：59b89a27c527ed00086d43dc
对于具有相同定义域 $D$ 的函数 $f\left(x\right)$ 和 $g\left(x\right)$，若存在函数 $h\left(x\right) = kx + b$（$k,b$ 为常数），对任给的正数 $m$，存在相应的 ${x_0} \in D$，使得当 $x \in D$ 且 $x > {x_0}$ 时，总有 $ {\begin{cases}
0 < f\left(x\right) - h\left(x\right) < m, \\
0 < h\left(x\right) - g\left(x\right) < m, \\
\end{cases}} $ 则称直线 $l:y = kx + b$ 为曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 的“分渐近线”．给出定义域均为 $D= \left\{ {x\left| \right.{x > 1} } \right\}$ 的四组函数中，曲线 $y = f\left(x\right)$ 与 $y = g\left(x\right)$ 存在“分渐近线”的是  \((\qquad)\)
A: $f\left(x\right) = {x^2}$，$g\left(x\right) = \sqrt x $
B: $f\left(x\right) = {10^{ - x}} + 2$，$g\left(x\right) = \dfrac{2x - 3}{x}$
C: $f\left(x\right)=\dfrac{{{x^2} + 1}}{x}$，$g\left(x\right) = \dfrac{x\ln x + 1}{\ln x}$
D: $f\left(x\right) = \dfrac{{2{x^2}}}{x + 1}$，$g\left(x\right) = 2\left(x - 1 - { {\mathrm{e }} ^{ - x}}\right)$
【难度】
【出处】
2010年高考福建卷（理）
【标注】
  • 方法
    >
    思考方式
    >
    信息迁移
  • 知识点
    >
    微积分初步
    >
    导数的运算
    >
    函数极限
【答案】
BD
【解析】
“分渐近线”有很强的几何意义：
$y=f(x)$ 的图象在直线 $y=h(x)$ 上方，$y=g(x)$ 的图象在直线 $y=h(x)$ 的下方，且两个函数的图象离 $y=h(x)$ 要多近有多近．
由此容易判断选项 A 不存在“分渐近线”；选项 BD 存在“分渐近线”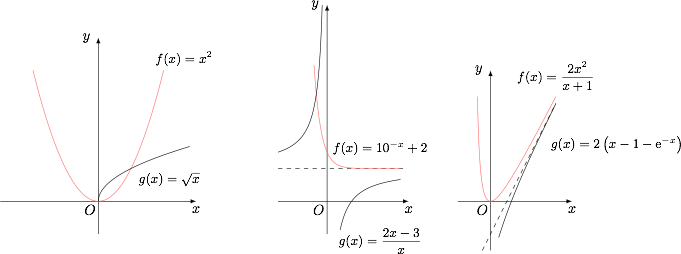．但对选项 C 就无法通过图象进行判断了．
下面对“分渐近线”进行进一步的研究．
对选项 D 图象的分析，以及条件\[ {\begin{cases}
0 < f\left(x\right) - h\left(x\right) < m, \\
0 < h\left(x\right) - g\left(x\right) < m, \\
\end{cases}} ,\]可得\[0<f(x)-g(x)<2m ,\]也就是 $f(x)-g(x)$ 从某处开始应该是恒正且无限接近于零的．
由此，对于选项 C，有$$f(x)-g(x)=\left(x+\dfrac 1x\right)-\left(x+\dfrac 1{\ln x}\right)=\dfrac 1x-\dfrac {1}{\ln x}=\dfrac {\ln x-x}{x\ln x}.$$我们熟知 $y=\ln x$ 比 $y=x$ 增长的慢，于是 $f(x)-g(x)$ 不满足某处开始恒正这一必要条件．
题目 答案 解析 备注
0.109628s