选修 4-1 几何证明选讲
如图，在 $\odot O$ 中，相交于点 $E$ 的两弦 $AB$，$CD$ 的中点分别是 $M$，$N$，直线 $MO$ 与直线 $CD$ 相交于点 $F$．证明：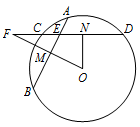
如图，在 $\odot O$ 中，相交于点 $E$ 的两弦 $AB$，$CD$ 的中点分别是 $M$，$N$，直线 $MO$ 与直线 $CD$ 相交于点 $F$．证明：
【难度】
【出处】
2015年高考湖南卷（理）
【标注】
-
$\angle MEN+\angle NOM=180^\circ$；标注答案略解析根据题意，得出 $ON\perp CD$ 和 $OM\perp AB$，再结合四边形内角和 $360^\circ$，问题即可解决．因为 $M$，$N$ 分别是两弦 $AB$，$CD$ 的中点，所以\[OM\perp AB,ON\perp CD,\]即\[\angle OME=90^\circ,\angle ONE=90^\circ,\]因此\[\angle OME+\angle ONE=180^\circ,\]又四边形的内角和等于 $360^\circ$，故\[\angle MEN+\angle NOM=180^\circ.\]
-
$FE\cdot FN=FM\cdot FO$．标注答案略解析由第一问可知 $E,M,O,N$ 四点共圆，结合割线定理，问题得证．由 $(1)$ 知，$O$，$M$，$E$，$N$ 四点共圆，如图所示，
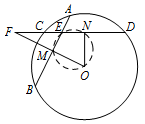故由割线定理，得 $FE\cdot FN=FM\cdot FO$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
