如图，$AB$ 是圆 $O$ 的直径，点 $C$ 是圆 $O$ 上异于 $A$，$B$ 的点，$PO$ 垂直于圆 $O$ 所在的平面，且 $PO=OB=1$．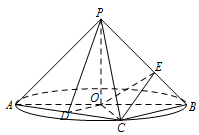
【难度】
【出处】
2015年高考福建卷（文）
【标注】
-
若 $D$ 为线段 $AC$ 的中点，求证：$AC\perp$ 平面 $PDO$；标注答案略解析需在平面 $PDO$ 内，找到两条相交直线与 $AC$ 垂直，为 $PO$ 和 $OD$．在 $\triangle AOC$ 中，因为 $OA=OC$，$D$ 为 $AC$ 的中点，所以 $AC\perp DO$．
又 $PO$ 垂直于圆 $O$ 所在的平面，所以 $PO\perp AC$．
因为 $DO\cap PO=O$，所以 $AC\perp 平面PDO$． -
求三棱锥 $P-ABC$ 体积的最大值；标注答案$\dfrac13$解析以 $\triangle ABC$ 为底面，三棱锥的高固定为 $1$，因此 $\triangle ABC$ 的面积越大，体积越大．因为点 $C$ 在圆 $O$ 上，所以当 $CO\perp AB$ 时，$C$ 到 $AB$ 的距离最大，且最大值为 $1$．
又 $AB=2$，所以 $\triangle ABC$ 面积的最大值为 $\dfrac 12\times 2\times 1=1$．
又因为三棱锥 $P-ABC$ 的高 $PO=1$，故三棱锥 $P-ABC$ 体积的最大值为 $\dfrac 13\times 1\times 1=\dfrac 13$． -
若 $BC=\sqrt 2$，点 $E$ 在线段 $PB$ 上，求 $CE+OE$ 的最小值．标注答案$\dfrac{\sqrt 2+\sqrt 6}2$解析通过题目描述确定出 $\triangle POB$ 和 $\triangle PBC$ 的信息，将 $\triangle PBC$ 绕 $PB$ 旋转到与 $PBO$ 共面，根据两点之间线段最短，求出最小值．
解法一：
在 $\triangle POB$ 中，$PO=OB=1$，$\angle POB=90^\circ$，所以 $PB=\sqrt{1^1+1^1}=\sqrt 2$．
同理 $PC=\sqrt 2$，所以 $PB=PC=BC$．
在三棱锥 $P-ABC$ 中，将侧面 $BCP$ 绕 $PB$ 旋转至平面 $BC'P$，使之与平面 $ABP$ 共面，如图所示．
当 $O$，$E$，$C'$ 共线时，$CE+OE$ 取得最小值．
又因为 $OP=OB$，$C'P=C'B$，所以 $OC'$ 垂直平分 $PB$，即 $E$ 为 $PB$ 的中点．
从而 $OC'=OE+EC'=\dfrac{\sqrt 2}2+\dfrac{\sqrt 6}2=\dfrac{\sqrt 2+\sqrt 6}2$，即 $CE+OE$ 的最小值为 $\dfrac{\sqrt 2+\sqrt 6}2$．解法二：
在 $\triangle POB$ 中，$PO=OB=1$，$\angle POB＝90^\circ$，所以 $\angle OPB＝45^\circ$，$PB=\sqrt {1^2+1^2}=\sqrt 2$．
同理，$PC=\sqrt 2$．所以 $PB=PC=BC$，因此 $\angle CPB＝60^\circ$．
在三梭锥 $P-ABC$ 中，将侧面 $BCP$ 绕 $PB$ 旋转至平面 $BC'P$，使之与平面 $ABP$ 共面，如图所示． 当 $O$，$E$，$C′$ 共线时，$CE＋OE$ 取得最小值．
所以在 $\triangle OC'P$ 中，由余弦定理得\[\begin{split}OC'^2&=1+2-2\times 1\times \sqrt 2\times \cos \left(45^\circ+60^\circ\right)\\&=1+2-2\sqrt 2\left(\dfrac {\sqrt 2}{2}\times \dfrac 12-\dfrac {\sqrt 2}{2}\times \dfrac {\sqrt 3}{2}\right)\\&=2+\sqrt 3.\end{split}\]从而 $OC'=\sqrt {2+\sqrt 3}=\dfrac{\sqrt 2+\sqrt 6}{2}$．
所以 $CE+OE$ 的最小值为 $\dfrac{\sqrt 2+\sqrt 6}2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
