已知双曲线 $E:\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\left(a > 0,b > 0\right)$ 的两条渐近线分别为 ${l_1}:y = 2x$，${l_2}:y = - 2x$．
【难度】
【出处】
无
【标注】
-
求双曲线 $E$ 的离心率；标注答案双曲线 $E$ 的离心率为 $\sqrt 5$．解析由渐近线方程得到关于 $a,b$ 的等式，结合 $a^2=b^2+c^2$，解出离心率 $e$ 即可．因为双曲线 $E$ 的渐近线分别为 $y=2x$，$y=-2x$，所以 $\dfrac b a =2$，结合 $a^2=b^2+c^2$ 和 $e=\dfrac c a $，可解得双曲线 $E$ 的离心率$e=\sqrt 5$．
-
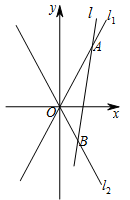
如图，$O$ 为坐标原点，动直线 $l$ 分别交直线 ${l_1}$，${l_2}$ 于 $A$，$B$ 两点（$A$，$B$ 分别在第一，四象限），且 $\triangle OAB$ 的面积恒为 $ 8 $，试探究：是否存在总与直线 $l$ 有且只有一个公共点的双曲线 $E$？若存在，求出双曲线 $E$ 的方程；若不存在，说明理由．
标注答案存在总与直线 $l$ 有且只有一个公共点的双曲线 $E$，双曲线的方程是 $\dfrac{x^2}{4} - \dfrac{y^2}{16} = 1$．解析假设存在，结合第一问可知，当直线 $l$ 变化时，满足题意的双曲线的半实轴长 $a$ 的值为定值．直线 $l$ 中会产生两个参数，因此，若能够从题中找出两个等式，将 $a$ 表示出来，并判断是否可化简为常数，是本题的主要思路．由（1）得 ${b^2} = 4{a^2}$，所以双曲线的方程为 $\dfrac{x^2}{a^2} - \dfrac{y^2}{{4{a^2}}} = 1$．
设直线 $l$ 的方程为 $x = my + t$，由题意\[ - \dfrac{1}{2} < m < \dfrac{1}{2}.\]由 $ \begin{cases}
x = my + t ,\\
y = 2x .\\
\end{cases} $ 得 ${y_1} = \dfrac{2t}{1 - 2m}$，同理可得\[{y_2} = \dfrac{ - 2t}{1 + 2m},\]设直线 $l$ 与 $x$ 轴交于点 $C,$ 则 $C\left(t,0\right)$．
所以\[ \begin{split}{S_{\triangle ABO}} &\overset{\left[a\right]}= \dfrac{1}{2}\left| {OC} \right| \cdot \left| {y_1 - y{}_2} \right| \\&= \dfrac{1}{2}\left| t \right| \cdot \left| {\dfrac{2t}{1 - 2m} - \dfrac{ - 2t}{1 + 2m}} \right| \\&= 8,\end{split} \]（推导中用到[a]）
即 ${t^2} = 4\left(1 - 4{m^2}\right)$，联立直线与双曲线方程，得\[ \begin{cases}
x = my + t ,\\
\dfrac{x^2}{a^2} - \dfrac{y^2}{{4{a^2}}} = 1.\\
\end{cases} \]整理，得\[\left(4{m^2} - 1\right){y^2} + 8mty + 4\left({t^2} - {a^2}\right) = 0,\]因为 $4{m^2} - 1 < 0$，直线与双曲线有且仅有一个公共点，当且仅当\[\Delta = 64{m^2}{t^2} - 16\left(4{m^2} - 1\right)\left({t^2} - {a^2}\right) = 0,\]即\[4{m^2}{a^2} + {t^2} - {a^2} = 0,\]将 $t^2=4\left(1-4m^2\right)$，代入得\[ \left(1 - 4{m^2}\right)\left({a^2} - 4\right) = 0,\]所以 ${a^2} = 4$．
因此，存在总与直线 $l$ 有且只有一个公共点的双曲线 $E$，双曲线的方程是 $\dfrac{x^2}{4} - \dfrac{y^2}{16} = 1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
