如图,三棱锥 $A - BCD$ 中,$AB \perp$ 平面 $ BCD $,$CD \perp BD$.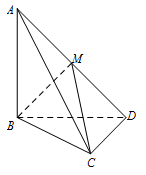

【难度】
【出处】
2014年高考福建卷(文)
【标注】
-
求证:$CD \perp $ 平面 $ABD$;标注答案略.解析在面上找两条相交直线均垂直于 $CD$ 即可.在三棱锥 $A - BCD$ 中,因为 $ AB \perp $ 平面 $BCD$,又 $ CD \subset 平面 BCD$,所以 $ AB \perp CD$.
又 $ BD \perp CD$,且 $BD \cap AB = B$,所以 $ CD \perp $ 平面 $ABD$. -
若 $AB = BD = CD = 1$,$M$ 为 $AD$ 中点,求三棱锥 $A - MBC$ 的体积.标注答案$\dfrac{1}{12}$.解析求三棱锥的体积问题,主要在于顶点的选取,选择高和底面面积均易处理的情况下的顶点为顶点.法一:
由 $AB\perp $ 平面 $BCD $,得 $AB \perp BD $,因为 $AB=BD=1 $,所以 $S_{\triangle ABD}=\dfrac 1 2 $.
因为 $M $ 是 $AD $ 中点,所以 $S_{\triangle ABM}=\dfrac 1 2 S_{\triangle ABD}=\dfrac 1 4 $.
由(1)知,$CD \perp平面 ABD$,所以 三棱锥 $ C-ABM$ 的高 $h=CD=1 $,
因此,三棱锥 $A-MBC $ 的体积为\[ V_{A-MBC}=V_{C-ABM}=\dfrac 1 3 S_{\triangle ABM}\cdot h=\dfrac 1 {12} .\]法二:
由 $AB\perp $ 平面 $ BCD $ 知,平面 $ABD \perp $ 平面 $ BCD $,
如图,过点 $ M $ 作 $MN \perp BD$ 交 $ BD $ 于点 $ N $, 又 $平面 ABD \cap 平面 BCD=BD $,则 $MN\perp 平面 BCD $,且\[MN=\frac{1}{2}AB=\frac{1}{2},\]又 $CD\perp BD$,$BD=CD=1$,所以\[{{S}_{\triangle BCD}}=\frac{1}{2},\]所以,三棱锥 $A-MBC$ 的体积\[\begin{split}{{V}_{A-MBC}} & ={{V}_{A-BCD}}-{{V}_{M-BCD}} \\& =\frac{1}{3}AB\cdot {{S}_{\triangle BCD}}-\frac{1}{3} MN \cdot {{S}_{\triangle BCD}} \\& =\frac{1}{12}.\end{split}\]
又 $平面 ABD \cap 平面 BCD=BD $,则 $MN\perp 平面 BCD $,且\[MN=\frac{1}{2}AB=\frac{1}{2},\]又 $CD\perp BD$,$BD=CD=1$,所以\[{{S}_{\triangle BCD}}=\frac{1}{2},\]所以,三棱锥 $A-MBC$ 的体积\[\begin{split}{{V}_{A-MBC}} & ={{V}_{A-BCD}}-{{V}_{M-BCD}} \\& =\frac{1}{3}AB\cdot {{S}_{\triangle BCD}}-\frac{1}{3} MN \cdot {{S}_{\triangle BCD}} \\& =\frac{1}{12}.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2