如图 $(1)$,在直角梯形 $ABCD$ 中,$AD \parallel BC$,$\angle BAD=\dfrac {\mathrm \pi} {2}$,$AB=BC=\dfrac 12AD=a$,$E$ 是 $AD$ 的中点,$O$ 是 $AC$ 与 $BE$ 的交点.将 $\triangle ABE$ 沿 $BE$ 折起到图 $(2)$ 中 $\triangle A_1BE$ 的位置,得到四棱锥 $A_1-BCDE$.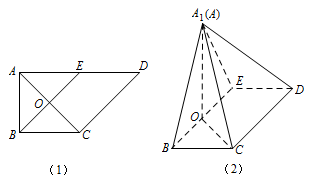

【难度】
【出处】
2015年高考陕西卷(文)
【标注】
-
证明:$CD\perp 平面A_1OC$;标注答案略解析注意折叠过程中 $BE$ 和 $AO,OC$ 的位置关系不变,然后通过证明 $BE\perp 面 AOC$ 来证明 $CD\perp 面 A_1OC$.在题图 $(1)$ 中,因为 $AB=BC=\dfrac 12AD=a$,$E$ 是 $AD$ 的中点,$\angle BAD=\dfrac {\mathrm \pi} {2}$,
所以 $BE\perp AC$.
即在题图 $(2)$ 中,$BE\perp A_1O$,$BE\perp OC$,
从而 $BE\perp 平面A_1OC$.
又 $CD \parallel BE$,
所以 $CD\perp 平面A_1OC$. -
若 $平面A_1BE\perp 平面BCDE$,四棱锥 $A_1-BCDE$ 的体积为 $36\sqrt 2$,求 $a$ 的值.标注答案$a=6$解析可由条件得知 $A_1O$ 为底面 $BCDE$ 上的高.然后利用棱锥体积公式计算即可.由已知,平面 $A_1BE\perp 平面BCDE$,且 $平面 A_1BE\cap 平面BCDE=BE$,
又由 $(1)$ 可得 $A_1O\perp BE$,
所以 $A_1O\perp 平面BCDE$.
即 $A_1O$ 是四棱锥$A_1-BCDE$ 的高.
由题图 $(1)$ 知,$A O=\dfrac {\sqrt 2}{2}AB=\dfrac {\sqrt 2}{2}a$,平行四边形 $BCDE$ 的面积 $S=BC\cdot AB=a^2$,
从而四棱锥 $A_1-BCDE$ 的体积为\[V=\dfrac 13S\cdot A_1O=\dfrac 13\times a^2\times \dfrac {\sqrt 2}{2}a=\dfrac {\sqrt 2}{6}a^3.\]由 $\dfrac {\sqrt 2}{6}a^3=36\sqrt 2$,得 $a=6$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2