如图,椭圆 $E$:$\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1\left(a>b>0\right)$ 经过点 $A\left(0,-1\right)$,且离心率为 $\dfrac {\sqrt 2}{2}$.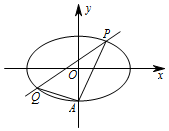

【难度】
【出处】
无
【标注】
-
求椭圆 $E$ 的方程;标注答案$\dfrac {x^2}{2}+ y^2=1$.解析本题考查椭圆的基本量.由题设知 $\dfrac ca=\dfrac {\sqrt 2}{2}$,$b=1$,结合 $a^2=b^2+c^2$,解得 $a=\sqrt 2$.
所以椭圆 $E$ 的方程为 $\dfrac {x^2}{2}+ y^2=1$. -
经过点 $\left(1,1\right)$,且斜率为 $k$ 的直线与椭圆 $E$ 交于不同的两点 $P$,$Q$(均异于点 $A$),证明:直线 $AP$ 与 $AQ$ 的斜率之和为 $2$.标注答案略.解析将直线 $PQ$ 的方程和椭圆方程联立,用韦达定理表达 $x_1+x_2$ 和 $x_1x_2$,然后计算 $k_{AP}+k_{AQ}$ 的值即可.由题设知,直线 $PQ$ 的方程为 $y=k\left(x-1\right)+1\left(k\neq 2\right)$,代入 $\dfrac {x^2}{2}+ y^2=1$,得\[\left(1+2k^2\right)x^2-4k\left(k-1\right)x+2k\left(k-2\right)=0.\]由已知 $\Delta >0$,设 $P\left(x_1,y_1\right)$,$Q\left(x_2,y_2\right)$,$x_1x_2\neq 0$,则\[x_1+x_2=\dfrac {4k\left(k-1\right)}{1+2k^2} , x_1x_2=\dfrac {2k\left(k-2\right)}{1+2k^2}.\]从而直线 $AP$,$AQ$ 的斜率之和为\[\begin{split}k_{AP}+k_{AQ}&=\dfrac {y_1+1}{x_1}+\dfrac {y_2+1}{x_2}\\&=\dfrac {kx_1+2-k}{x_1}+\dfrac {kx_2+2-k}{x_2}\\&=2k+\left(2-k\right)\left(\dfrac {1}{x_1}+\dfrac {1}{x_2}\right)\\&=2k+\left(2-k\right)\dfrac {x_1+x_2}{x_1x_2}\\&=2k+\left(2-k\right)\dfrac {4k\left(k-1\right)}{2k\left(k-2\right)}\\&=2k-2\left(k-1\right)\\&=2.\end{split}\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2