如图,$AB$ 切 $\odot O$ 于点 $B$,直线 $AO$ 交 $\odot O$ 于 $D$,$E$ 两点,$BC\perp DE$,垂足为 $C$.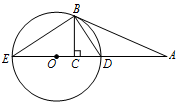

【难度】
【出处】
2015年高考陕西卷(理)
【标注】
-
证明:$\angle CBD=\angle DBA$;标注答案略解析可通过 $\angle E$ 的传递来证 $\angle CBD=\angle DBA$.因为 $DE$ 为 $\odot O$ 直径,
所以 $\angle BED+\angle EDB=90^\circ$,
又 $BC\perp DE$,
所以 $\angle CBD+\angle EDB=90^\circ$,
从而 $\angle CBD=\angle BED$.
又 $AB$ 切 $\odot O$ 于点 $B$,得 $\angle DBA= \angle BED$,
所以 $\angle CBD=\angle DBA$. -
若 $AD=3DC$,$BC=\sqrt 2$,求 $\odot O$ 的直径.标注答案$3$解析对 $\angle ABC$ 应用角平分线定理,并结合已知可求出 $AD$ 和 $AB$,然后用圆幂定理求出直径.由 $(1)$ 知 $BD$ 平分 $\angle CBA$,则 $\dfrac {BA}{BC}=\dfrac {AD}{CD}=3$.
又 $BC=\sqrt 2$,
从而 $AB=3\sqrt 2$.
所以 $AC=\sqrt {AB^2-BC^2}=4$,
所以 $AD=3$.
由切割线定理,得 $AB^2=AD\cdot AE$,即 $AE=\dfrac {AB^2}{AD}=6$,
故 $DE=AE-AD=3$,即 $\odot O$ 的直径为 $3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2