如图,在 $\triangle ABC$ 中,$\angle ABC = 90^\circ $,$AB = \sqrt 3 $,$BC = 1$,$P$ 为 $\triangle ABC$ 内一点,$\angle BPC = 90^\circ $.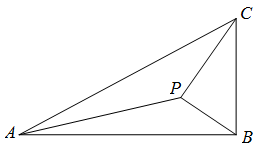

【难度】
【出处】
无
【标注】
-
若 $PB = \dfrac{1}{2}$,求 $PA$;标注答案$\dfrac{\sqrt 7 }{2}$解析本题考查余弦定理的应用.选择合适的三角形求解即可.由已知得 $\angle PBC = 60^\circ $,所以\[\angle PBA = 30^\circ .\]在 $\triangle PBA$ 中,由余弦定理得\[\begin{split}P{A^2} = 3 + \dfrac{1}{4} - 2 \times \sqrt 3 \times \dfrac{1}{2}\cos 30^\circ= \dfrac{7}{4},\end{split}\]故\[PA = \dfrac{\sqrt 7 }{2}.\]
-
若 $\angle APB = 150^\circ $,求 $\tan \angle PBA$.标注答案$ \dfrac{\sqrt 3 }{4}$解析本题考查正弦定理的应用.设 $\angle PBA = \alpha $,由已知得\[PB = \sin \alpha .\]在 $\triangle PBA$ 中.由正弦定理得\[\dfrac{\sqrt 3 }{\sin 150^\circ } = \dfrac{\sin \alpha }{{\sin \left( {30^\circ - \alpha } \right)}},\]化简得\[\sqrt 3 \cos \alpha = 4\sin \alpha ,\]所以\[\tan \alpha = \dfrac{\sqrt 3 }{4},\]即\[\tan \angle PBA = \dfrac{\sqrt 3 }{4}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2