四边形 $ABCD$ 的内角 $A$ 与 $C$ 互补，$AB = 1$，$BC = 3$，$CD = DA = 2$．
【难度】
【出处】
2014年高考新课标Ⅱ卷（文）
【标注】
-
求 $C$ 和 $BD$；标注答案$C = {60 ^\circ }$；$BD = \sqrt 7$解析本题考查正余弦定理的相关知识．确定合适的三角形进行求解是解决本题的关键．如图：
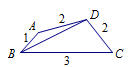由题设及余弦定理得\[\begin{split}B{D^2} &= B{C^2} + C{D^2} - 2BC \cdot CD\cos C \\& =13 - 12\cos C, \quad \cdots \cdots ① \\ B{D^2} &= A{B^2} + D{A^2} - 2AB \cdot DA\cos A \\& \overset{\left[a\right]}= 5 + 4\cos C. \quad \cdots \cdots ② \end{split}\]（推导中用到[a]）．
由 $ ①② $ 得 $\cos C = \dfrac{1}{2}$，故 $C = {60 ^\circ }$，$BD = \sqrt 7$． -
求四边形 $ABCD$ 的面积．标注答案$2\sqrt 3 $解析本题考查三角形面积的计算公式．将四边形分割成两个三角形求解．四边形 $ ABCD $ 的面积为\[\begin{split}S & \overset{\left[a\right]}= \dfrac{1}{2}AB \cdot DA\sin A + \dfrac{1}{2}BC \cdot CD\sin C \\&= \left(\dfrac{1}{2} \times 1 \times 2 + \dfrac{1}{2} \times 3 \times 2\right)\sin {60^\circ} \\&= 2\sqrt 3 .\end{split}\]（推导中用到[a]）
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
