如图，四棱锥 $P - ABCD$ 中，底面 $ABCD$ 为矩形，$PA \perp $ 平面 $ABCD$，$E$ 是 $PD$ 的中点．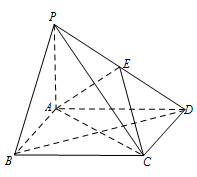
【难度】
【出处】
2014年高考新课标Ⅱ卷（文）
【标注】
-
证明：$PB\parallel $ 平面 $AEC$；标注答案略解析本题考查线面平行的证明定理．如图，设 $ BD $ 与 $ AC $ 的交点为 $ O $，连接 $ EO $．
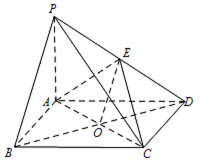因为 $ ABCD $ 为矩形，所以 $ O $ 为 $ BD $ 的中点，
又 $ E $ 为 $ PD $ 的中点，所以 $ EO \parallel PB $．
因为 $ EO \subset $ 平面 $ AEC $，$ PB \not\subset $ 平面 $ AEC $，
所以 $ PB \parallel $ 平面 $ AEC $． -
设 $AP = 1$，$AD = \sqrt 3 $，三棱锥 $P - ABD$ 的体积 $V = \dfrac{\sqrt 3 }{4}$，求 $A$ 到平面 $PBC$ 的距离．标注答案$\dfrac{{3\sqrt {13} }}{13}$解析本题考查空间中点到面的距离，可以考虑构造线段，也可以借助等体积法进行求解．因为\[V_{P - ABD}\overset{\left[a\right]}= \dfrac{1}{6}PA \cdot AB \cdot AD = \dfrac{\sqrt 3 }{6}AB.\]（推导中用到[a]）．
由 $V_{P - ABD} = \dfrac{\sqrt 3 }{4}$，可得 $AB = \dfrac{3}{2}$．
如图，作 $AH \perp PB$，交 $PB$ 于 $H$．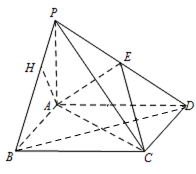
由题设知 $BC \perp $ 平面 $PAB$，所以 $BC \perp AH$，故 $AH \perp $ 平面 $PBC$．
又\[AH = \dfrac{PA \cdot AB}{PB} = \dfrac{{3\sqrt {13} }}{13}.\]所以 $ A $ 到平面 $ PBC $ 的距离为 $\dfrac{{3\sqrt {13} }}{13}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
