如图,四棱锥 $P-ABCD$ 的底面 $ABCD$ 是平行四边形,$BA = BD = \sqrt 2 $,$AD = 2$,$PA = PD = \sqrt 5 $,$E,F$ 分别是棱 $AD,PC$ 的中点.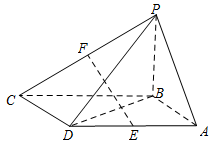

【难度】
【出处】
2014年高考天津卷(文)
【标注】
-
证明:$EF\parallel $ 平面 $PAB$;标注答案略解析本题考查线面平行判定定理.如图,取 $PB$ 中点 $M$,连接 $FM$,
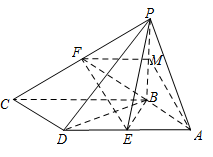 因为 $F$ 为 $PC$ 中点,所以 $ FM $ 为 $ \triangle PBC $ 的中位线,
因为 $F$ 为 $PC$ 中点,所以 $ FM $ 为 $ \triangle PBC $ 的中位线,
所以 $ FM \parallel BC \parallel AE $ 且 $FM = \dfrac{1}{2}BC = AE$,
所以四边形 $ EFMA $ 为平行四边形,$EF \parallel AM $.
因为 $ EF \not\subset $ 平面 $ PAB $,$ AM \subset $ 平面 $ PAB $,所以 $ EF \parallel $ 平面 $PAB$. -
若二面角 $P - AD - B$ 为 ${60^ \circ }$,
① 证明:平面 $PBC \perp $ 平面 $ABCD$;
② 求直线 $EF$ 与平面 $PBC$ 所成角的正弦值.标注答案① 略;
② $ \dfrac{2\sqrt{11}}{11} $解析本题考查面面垂直判定定理以及线面角的计算.① 连接 $ PE,BE $.
因为 $ PA=PD$,$BA=BD $,而 $ E $ 为 $ AD $ 中点,故 $ PE\perp AD$,$BE\perp AD $,所以 $ \angle PEB $ 为二面角 $ P-AD-B $ 的平面角.
在 $\triangle PAD $ 中,由\[AD = 2,PA = PD = \sqrt 5 ,\]可解得\[ PE=2 .\]$\triangle ABD $ 中,由\[BA = BD = \sqrt 2 ,\]可解得\[ BE=1.\]在三角形 $ PEB $ 中,$ PE=2 $,$BE=1$,$\angle PEB={{60}^{\circ }} $,由余弦定理,可解得\[ PB=\sqrt{3},\]从而 $ \angle PBE={{90}^{\circ }} $,即 $ BE\perp PB $,
又 $ BC\parallel AD$,$BE\perp AD $,从而 $ BE\perp BC $,因此 $ BE\perp $ 平面 $ PBC $.
又 $ BE\subset $ 平面 $ ABCD $,所以平面 $ PBC\perp $ 平面 $ ABCD $;
② 连接 $ BF $,由 ① 知 $ BE\perp $ 平面 $ PBC $.
所以 $ \angle EFB $ 为直线 $ EF $ 与平面 $ PBC $ 所成的角,由\[ PB=\sqrt{3},PA=\sqrt{5},AB=\sqrt{2} ,\]得 $ \angle ABP $ 为直角,而\[ MB=\frac{1}{2}PB=\frac{\sqrt{3}}{2} ,\]可得 $ AM=\dfrac{\sqrt{11}}{2} $,故 $ EF=\dfrac{\sqrt{11}}{2} $.又 $ BE=1 $,故在 ${\mathrm{Rt}} \triangle EBF $ 中,可得\[ \sin \angle EFB=\frac{BE}{EF}=\frac{2\sqrt{11}}{11} .\]所以,直线 $ EF $ 与平面 $ PBC $ 所成角的正弦值为 $ \dfrac{2\sqrt{11}}{11} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2