如图,已知双曲线 $C:\dfrac{x^2}{a^2} - {y^2} = 1\left(a > 0\right)$ 的右焦点为 $ F $.点 $ A$,$B $ 分别在 $ C $ 的两条渐近线上,$AF \perp x$ 轴,$AB \perp OB$,$BF\parallel OA$($ O $ 为坐标原点).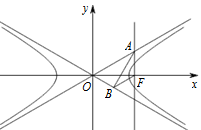

【难度】
【出处】
无
【标注】
-
求双曲线 $ C $ 的方程;标注答案$\dfrac{x^2}{3}-y^2=1$.解析本题考查双曲线的方程.因为直线 $OA $ 的方程为 $y=\dfrac{1}{a}x $,所以 $ A\left(c,\dfrac{c}{a}\right)$,
因为直线 $ OB$ 的方程为 $y=-\dfrac{1}{a}x $,设 $B\left(t, - \dfrac{t}{a} \right) $,
又 $F\left(c,0\right) $,$AB \perp OB$,$BF\parallel OA$.由直线间的位置关系得\[ \begin{cases} \dfrac{{\dfrac{c + t}{a}}}{c - t} \cdot \dfrac{ - 1}{a} = - 1,\\\dfrac{1}{a}=\dfrac{t}{a\left(c-t\right)}.\end{cases} \]解得\[ \begin{cases}t=\dfrac{c}{2},\\a=\sqrt3.\end{cases} \]所以,双曲线的方程为\[ \dfrac{x^2}{3}-y^2=1.\] -
过 $ C $ 上一点 $P\left({x_0},{y_0}\right)\left({y_0} \ne 0\right)$ 的直线 $l:\dfrac{{{x_0}x}}{a^2} - {y_0}y = 1$,与直线 $ AF $ 相交于点 $ M $,与直线 $x = \dfrac{3}{2}$ 相交于点 $ N $.证明:当点 $ P $ 在 $ C $ 上移动时,$\dfrac{{\left| {MF} \right|}}{{\left| {NF} \right|}}$ 恒为定值,并求此定值.标注答案证明略;定值为 $\dfrac{2\sqrt 3 }{3} $.解析本题利用点 $P$ 的坐标表示所求比值,进而证明求解这个比值为定值.由(1)知 $ l:\dfrac{{{x_0}x}}{3} - {y_0}y = 1,F\left(2,0\right) $,结合题意得 $ M\left(2,\dfrac{{2{x_0} - 3}}{{3{y_0}}}\right) $,$ N\left(\dfrac{3}{2},\dfrac{{{x_0} - 2}}{{2{y_0}}}\right) $,
所以\[ \begin{split}\dfrac{|MF|}{|NF|}&\overset{\left[a\right]}= \dfrac{{\left| {\dfrac{{2{x_0} - 3}}{{3{y_0}}}} \right|}}{{\sqrt {\dfrac{1}{4} + {{\left(\dfrac{{{x_0} - 2}}{{2{y_0}}}\right)}^2}} }} \\& = \dfrac{{2\left| {2{x_0} - 3} \right|}}{{3\sqrt {y_0^2 + {{\left({x_0} - 2\right)}^2}} }}
\\& = \dfrac{{2\left| {2{x_0} - 3} \right|}}{{3\sqrt {{\dfrac{x_0^2}{3}} - 1 + {{\left({x_0} - 2\right)}^2}} }} \\& = \dfrac{{2\left| {2{x_0} - 3} \right|}}{{3\dfrac{{\left| {2{x_0} - 3} \right|}}{\sqrt 3 }}} \\& = \dfrac{2\sqrt 3 }{3} .\end{split} \](推导中用到[a])
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2