查看数据源：59cca33e310996000b86b2d3
四面体 $ABCD$ 的六条棱的棱长构成集合 $\{1,2\}$，则四面体 $ABCD$ 的体积可能取值为 \((\qquad)\)
A: $\dfrac{\sqrt{11}}{6}$
B: $\dfrac{\sqrt {11}}{12}$
C: $\dfrac{\sqrt {14}}{12}$
D: 以上答案都不对
【难度】
【出处】
无
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
【答案】
ABC
【解析】
注意到四面体 $ABCD$ 必然有一个面的三边边长分别为 $2,2,1$，于是在此基础上确定一个固定的底面，然后就顶点到底面三个顶点的距离展开讨论．如图，体积的所有可能取值为 $\dfrac{\sqrt{11}}{6},\dfrac{\sqrt {11}}{12},\dfrac{\sqrt {14}}{12}$．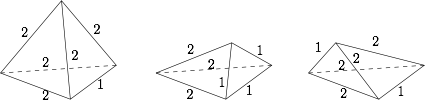
题目 答案 解析 备注
0.118429s