如图,三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,$A{A_1} \perp BC$,${A_1}B \perp B{B_1}$.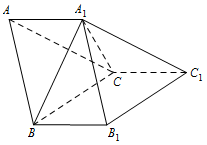

【难度】
【出处】
2014年高考江西卷(文)
【标注】
-
求证:${A_1}{C} \perp C{C_1}$;标注答案略解析本题考查异面直线垂直的证明问题,借助线面垂直进行证明.三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中,
$\because A{A_1} \perp BC$,$\therefore B{B_1} \perp BC$.
又 $B{B_1} \perp {A_1}B$,且 $BC \cap {A_1}B = B$,
$\therefore B{B_1} \perp 面 BC{A_1}$.
又 $B{B_1}\parallel C{C_1}$,$\therefore C{C_1} \perp 面 BC{A_1}$.
又 $ A_1{C} \subset 面 BC{A_1}$,
$\therefore$ ${A_1}C \perp C{C_1}$. -
若 $AB = 2$,$AC = \sqrt 3$,$BC = \sqrt 7 $,问 $A{A_1}$ 为何值时,三棱柱 $ABC - {A_1}{B_1}{C_1}$ 体积最大,并求此最大值.标注答案当 $ A { A _1} = \dfrac{{\sqrt {42} }}{7}$ 时,三棱柱 $ABC - {A_1}{B_1}{C_1}$ 体积最大,最大值为 $\dfrac{3\sqrt 7 }{7}$解析本题考查三棱柱的体积计算,把体积表示为棱长的函数,研究其最值.设 $A{A_1} = x $,在 ${\mathrm{Rt}}\triangle {A_1}B{B_1}$ 中,\[A_1B = \sqrt {{A_1}B_1^2 - BB_1^2} = \sqrt {4 - {x^2}} ,\]同理,\[{A_1} C = \sqrt {{A_1}C_1^2 - CC_1^2} = \sqrt {3 - {x^2}} ,\]在 $\triangle {A_1}BC$ 中,\[\begin{split}\cos \angle B{A_1}C & \overset{\left[a\right]}= \dfrac{{{A_1}{B^2} + {A_1}{C^2} - B{C^2}}}{{2{A_1}B \cdot {A_1}C}} \\& = - \dfrac{x^2}{{\sqrt {\left(4 - {x^2}\right)\left(3 - {x^2}\right)} }},\\ \sin \angle B{A_1}C & = \sqrt {\dfrac{{12 - 7{x^2}}}{{\left(4 - {x^2}\right)\left(3 - {x^2}\right)}}} ,\end{split}\](推导中用到[a]).
所以由三角形面积公式得\[\begin{split}{S_{\triangle {A_1}BC}} & = \dfrac{1}{2}{A_1}B \cdot {A_1}C \cdot \sin \angle B{A_1}C \\& = \dfrac{{\sqrt {12 - 7{x^2}} }}{2},\end{split}\]从而三棱柱 $ABC - {A_1}{B_1}{C_1}$ 的体积\[\begin{split}V &\overset{\left[a\right]}= {S_{\triangle {A_1}BC}} \cdot A{A_1} \\& = \dfrac{{x\sqrt {12 - 7{x^2}} }}{2}\\&=\dfrac 12 \sqrt {12{x^2} - 7{x^4}} \\& =\dfrac 12 \sqrt { - 7\left({x^2} - \dfrac{6}{7}\right)^2 + \dfrac{36}{7}} ,\end{split}\](推导中用到[a]).
故当 $x = \dfrac{{\sqrt {42} }}{7}$,即 $ A { A _1} = \dfrac{{\sqrt {42} }}{7}$ 时,三棱柱 $ABC - {A_1}{B_1}{C_1}$ 体积最大,最大值为 $\dfrac{3\sqrt 7 }{7}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2