如图,已知抛物线 $C:{x^2} = 4y$,过点 $M\left(0,2\right)$ 任作一直线与 $C$ 相交于 $A$,$B$ 两点,过点 $B$ 作 $y$ 轴的平行线与直线 $AO$ 相交于点 $D$($O$ 为坐标原点).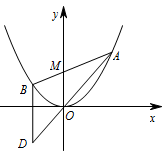

【难度】
【出处】
无
【标注】
-
证明:动点 $D$ 在定直线上;标注答案略解析本题解决关键是求解动点 $D$ 的坐标,探究其所满足的轨迹是否为直线.根据题意可设 $ AB $ 方程为 $ y=kx+2 $,代入 ${x^2} = 4 y $,整理得\[{x^2} - 4 kx - 8 = 0 .\]设 $A \left({x_1},{ y _1}\right)$,$B\left({x_2},{ y _2}\right)$,则有\[{x_1}{x_2} \overset{\left[a\right]}=-8,\](推导中用到[a]).
直线 $ AO $ 的方程为\[ y = \dfrac{ y_1}{x_1}x,\]$ BD $ 的方程为\[x = {x_2},\]联立解得交点 $ D $ 的坐标为\[
\left( x_2 ,\dfrac{{{ y _1}{x_2}}}{x_1}\right)\]注意到 ${x_1}{x_2} =-8$ 及 $x_1^2 = 4{ y_1}$,则 $D $ 的纵坐标为\[ \dfrac{{{ y_1}{x_1}{x_2}}}{x_1^2} = \dfrac{{ - 8 { y_1}}}{{4{ y_1}}} =-2,\]因此 $ D $ 点在定直线 $ y=-2 $ 上 $\left(x \ne 0\right)$. -
作 $C$ 的任意一条切线 $l$(不含 $x$ 轴),与直线 $y = 2$ 相交于点 ${N_1}$,与(1)中的定直线相交于点 ${N_2}$,证明:${\left|{M{N_2}}\right|}^2 - |M{N_1}|^2$ 为定值,并求此定值.标注答案证明略;定值为 $ 8 $解析本题是直线与圆锥曲线的定值问题,将所求利用直线的参数进行表示,证明其为定值.依据题设,切线 $ l $ 的斜率存在且不等于 $ 0 $,设切线 $ l $ 的方程为 $y=ax+b\left(a \ne 0\right)$,
代入 ${x^2} = 4 y $得\[{x^2} - 4ax - 4b = 0,\]由 $\Delta=0 $ 得\[16{a^2} + 16b = 0,\]化简整理得\[b = - {a^2},\]故切线 $ l $ 的方程可写为\[y = ax - {a^2}.\]分别令 $ y=2、y=-2 $ 得 ${N_1}、{N_2}$ 的坐标为\[{N_1}\left(\dfrac{2}{a} + a,2\right),{N_2}\left( - \dfrac{2}{a} + a, - 2\right),\]则\[\begin{split}{\left| {\left. {M{N_2}} \right|} \right.^2} - {\left| {\left. {M{N_1}} \right|} \right.^2} &\overset{\left[a\right]}= {\left(\dfrac{2}{a} - a\right)^2} + {4^2} - {\left(\dfrac{2}{a} + a\right)^2} \\&= 8,\end{split}\](推导中用到[a]),即 ${\left| {\left. {M{N_2}} \right|} \right.^2} - {\left| {\left. {M{N_1}} \right|} \right.^2}$ 为定值 $ 8 $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2