如图，三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，侧棱 ${A_1}A \perp $ 底面 $ABC$，且各棱长均相等，$D$，$E$，$F$ 分别为棱 $AB$，$BC$，${A_1}{C_1}$ 的中点．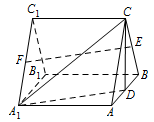
【难度】
【出处】
2013年高考天津卷（文）
【标注】
-
证明 $EF\parallel $ 平面 ${A_1}CD$；标注答案略解析本题考查线面平行的判定定理．在面上在一条直线平行于已知直线即可．如图，连接 $ED$．
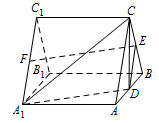在三棱柱 $ABC - {A_1}{B_1}{C_1}$ 中，$AC\parallel {A_1}{C_1}$，且 $AC = {A_1}{C_1}$，
在 $\triangle ABC$ 中，因为 $D,E$ 分别为 $AB,BC$ 的中点，所以 $DE = \dfrac{1}{2}AC$，且 $DE\parallel AC$．
又因为 $F$ 为 ${A_1}{C_1}$ 的中点，可得 ${A_1}F = DE$，且 ${A_1}F\parallel DE$，即四边形 ${A_1}DEF$ 为平形四边形，所以 $EF\parallel D{A_1}$．
又 $EF \not\subset $ 平面 ${A_1}CD$，$D{A_1} \subset $ 平面 ${A_1}CD$，所以 $EF\parallel $ 平面 ${A_1}CD$． -
证明平面 ${A_1}CD \perp $ 平面 ${A_1}AB{B_1}$；标注答案略解析本题考查面面垂直的判定定理的应用．其中一个面上存在一条直线垂直于另一个平面即可．由于底面 $ABC$ 是正三角形，$D$ 为 $AB$ 的中点，故 $CD \perp AB$．
又由于侧棱 ${A_1}A \perp $ 底面 $ABC$，$CD \subset $ 平面 $ABC$，所以 ${A_1}A \perp CD$．
又 ${A_1}A \cap AB = A$，因此 $CD \perp $ 平面 ${A_1}AB{B_1}$．而 $CD \subset $ 平面 ${A_1}CD$，所以 $平面{A_1}CD \perp 平面 {A_1}AB{B_1}$． -
求直线 $BC$ 与平面 ${A_1}CD$ 所成角的正弦值．标注答案$\dfrac{\sqrt 5 }{5}$解析本题考查线面角的计算．如图，在平面 ${A_1}AB{B_1}$ 内，过点 $B$ 作 $BG \perp {A_1}D$ 交直线 ${A_1}D$ 于点 $G$，连接 $CG$．
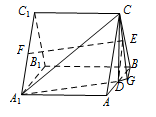由于平面 ${A_1}CD \perp $ 平面 ${A_1}AB{B_1}$，而直线 ${A_1}D$ 是平面 ${A_1}CD$ 与平面 ${A_1}AB{B_1}$ 的交线，故 $BG \perp $ 平面 ${A_1}CD$．
由此可得 $\angle BCG$ 为直线 $BC$ 与平面 ${A_1}CD$ 所成的角．
设棱长为 $a$，可得\[{A_1}D = \dfrac{\sqrt 5 a}{2},\]由 $\triangle {A_1}AD \backsim \triangle BGD$，易得\[BG = \dfrac{\sqrt 5 a}{5},\]在 $\operatorname{Rt} \triangle BGC$ 中，\[\sin \angle BCG = \dfrac{BG}{BC} = \dfrac{\sqrt 5 }{5}.\]所以直线 $BC$ 与平面 ${A_1}CD$ 所成角的正弦值为 $\dfrac{\sqrt 5 }{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
