从某企业生产的某种产品中抽取 $ 100 $ 件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：\[ \begin{array}{|c|c|c|c|c|c|} \hline
质量指标值分组 & \left[75,85\right)& \left[85,95\right)& \left[95,105\right)& \left[105,115\right)& \left[115,125\right)\\ \hline
频数 & 6 & 26 & 38 & 22 & 8 \\ \hline \end{array} \]
质量指标值分组 & \left[75,85\right)& \left[85,95\right)& \left[95,105\right)& \left[105,115\right)& \left[115,125\right)\\ \hline
频数 & 6 & 26 & 38 & 22 & 8 \\ \hline \end{array} \]
【难度】
【出处】
2014年高考新课标Ⅰ卷（文）
【标注】
-
在相应位置上作出这些数据的频率分布直方图；
标注答案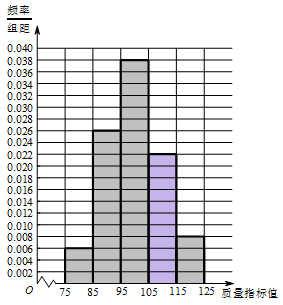
解析本题考查频率分布直方图的画法．根据题中数据得出对应的质量指标值．计算可得各组数据的频率分别为 $0.06,0.26,0.38,0.22,0.08 $，组距为 $ 10 $，故频率分布直方图中各组数据的纵坐标分别为 $ 0.006,0.026,0.038,0.022,0.008 $，得频率分布直方图如下： -
估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；标注答案$ \overline x = 100 $；$ {s^2} = 104 $．解析本题考查数据平均数、方差的计算方法．质量指标值的样本平均数为\[\begin{split}\overline x &= \dfrac{80 \times 6 + 90 \times 26 + 100 \times 38 + 110 \times 22 + 120 \times 8}{100} \\&= 100,\end{split}\]质量指标值的样本方差为\[\begin{split}{s^2} &= {\left( { - 20} \right)^2} \times 0.06 + {\left( { - 10} \right)^2} \times 0.26 + 0 \times 0.38 + {10^2} \times 0.22 + {20^2} \times 0.08 \\&= 104.\end{split}\]
-
根据以上抽样调查数据，能否认为该企业生产的这种产品符合"质量指标值不低于 $ 95 $ 的产品至少要占全部产品的 $ 80\% $”的规定？标注答案不符合解析本题考查用样本估计总体的相关知识．计算出质量指标值所占比例的估算值的百分比．依题意，质量指标值不低于 $ 95 $ 的产品所占比例的估计值为\[\dfrac{38 + 22 + 8}{100} = 68\% ,\]由于 $68\%< 80\% $，所以该企业生产的这种产品不符合"质量指标值不低于 $ 95 $ 的产品至少要占全部产品的 $ 80\% $ "的规定．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
