如图,三棱柱 $ABC-{A_1}{B_1}{C_1} $ 中,侧面 $B{B_1}{C_1}C $ 为菱形,${B_1}C $ 的中点为 $O $,且 $AO\perp $ 平面 $B{B_1}{C_1}C $.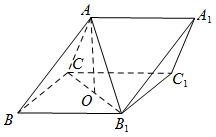

【难度】
【出处】
2014年高考新课标Ⅰ卷(文)
【标注】
-
证明:${B_1}C\perp AB $;标注答案略解析本题要证三角形 $ACB_1$ 为等腰三角形,可尝试利用证明三线合一的方式进行.如图,连接 $BC_1 $.
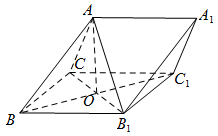 因为 $AO\perp $ 平面 $B{B_1}{C_1}C$,且 ${B_1}C \subset $ 平面 $B{B_1}{C_1}C$,
因为 $AO\perp $ 平面 $B{B_1}{C_1}C$,且 ${B_1}C \subset $ 平面 $B{B_1}{C_1}C$,
所以 $AO \perp {B_1}C$.
又因侧面 $B{B_1}{C_1}C $ 为菱形,
所以 $B{C_1} \perp {B_1}C$.
因为 $AO \cap B{C_1} = O$,
所以 ${B_1}C \perp $ 平面 $ABO$,
而 $AB\subset 平面 ABO$,所以 ${B_1}C \perp AB$. -
若 $AC\perp A{B_1}$,$ \angle CB{B_1} = 60^\circ$,$BC = 1$,求三棱柱 $ABC-{A_1}{B_1}{C_1} $ 的高.标注答案$\dfrac{{\sqrt {21} }}{7}$解析本题考查三棱柱的高的计算,可考虑等体积法进行求解.因为 $AO\perp $ 平面 $B{B_1}{C_1}C$,
所以 $AO \perp BO$.
又 $\angle CB{B_1} = 60^\circ$,$BC = 1 $,所以 $BO = \dfrac{\sqrt 3 }{2}$.
因为 $AC\perp A{B_1}$,所以\[AC = A{B_1} = \dfrac{\sqrt 2 }{2} , AO = \dfrac{1}{2},\]所以\[AB = \sqrt[{}]{{A{O^2} + {OB^2}}} = 1,\]易得\[{S_{\triangle ABC}} = \dfrac{\sqrt 7 }{8}.\]又 ${S_{\triangle CB{B_1}}} = \dfrac{\sqrt 3 }{4}$,所以\[\begin{split}{V_{A - B{B_1}C}} &\overset{\left[a\right]}= \dfrac 13 \cdot S_{\triangle{CBB_1}}\cdot OA\\&=\dfrac{\sqrt 3 }{24}.\end{split}\](推导中用到:$\left[a\right]$)
因为 ${V_{B_1 - A{B}C}} = {V_{A - B{B_1}C}}$,设三棱锥 $ {B_1 - A{B}C} $ 的高为 $h$,则\[\dfrac{1}{3}\cdot h\cdot {S_{\triangle ABC}} = \dfrac{\sqrt 3 }{24},\]解得 $h = \dfrac{{\sqrt {21} }}{7}$,所以三棱柱 $ABC-{A_1}{B_1}{C_1} $ 的高是 $\dfrac{{\sqrt {21} }}{7}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2