如图，已知二面角 $\alpha - MN - \beta $ 的大小为 ${60^ \circ }$，菱形 $ABCD$ 在面 $\beta $ 内，$A$，$B$ 两点在棱 $MN$ 上，$\angle BAD = {60^ \circ }$，$E$ 是 $AB$ 的中点，$DO \perp 面 \alpha $，垂足为 $O$．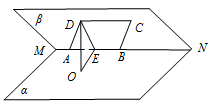
【难度】
【出处】
2014年高考湖南卷（文）
【标注】
-
证明：$AB \perp 平面 ODE$；标注答案略．解析在平面中找到两条相交直线均垂直于 $AB$ 即可．如图，因为 $DO \perp \alpha $，$AB \subset \alpha $，所以 $DO \perp AB$．连接 $BD$．
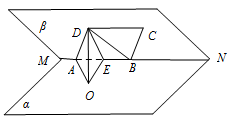由题设可知 $\triangle ABD$ 是正三角形，又 $E$ 是 $AB$ 的中点，所以 $DE \perp AB$，而 $DO \cap DE = D$，故 $AB \perp 平面 ODE$． -
求异面直线 $BC$ 与 $OD$ 所成角的余弦值．标注答案$\dfrac{3}{4}$．解析将异面直线平移到共线是求异面直线所成角的关键．因为 $BC\parallel AD$，所以 $BC$ 与 $OD$ 所成的角等于 $AD$ 与 $OD$ 所成的角，即 $\angle ADO$ 是 $BC$ 与 $OD$ 所成的角．
由（1）可知，$AB \perp 平面 ODE$，所以 $AB \perp OE$．
又 $DE \perp AB$，于是 $\angle DEO$ 是二面角 $\alpha - MN - \beta $ 的平面角，从而\[\angle DEO = {60^\circ}.\]不妨设 $AB = 2$，则 $AD = 2$，易知\[DE = \sqrt 3.\]在 ${\mathrm{Rt}}\triangle DOE$ 中，\[DO = DE\cdot \sin {60^\circ} = \dfrac{3}{2}.\]连接 $AO$，在 ${\mathrm{Rt}}\triangle AOD$ 中，\[\cos \angle ADO = \dfrac{DO}{AD} = \dfrac{{\frac{3}{2}}}{2} = \dfrac{3}{4},\]所以异面直线 $BC$ 与 $OD$ 所成角的余弦值为 $\dfrac{3}{4}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
