如图,在平面四边形 $ABCD$ 中,$DA \perp AB$,$DE = 1$,$EC = \sqrt 7 $,$EA = 2$,$\angle ADC = \dfrac{{2{\mathrm \pi} }}{3}$,$\angle BEC = \dfrac{{\mathrm \pi} }{3}$.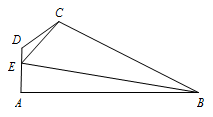

【难度】
【出处】
2014年高考湖南卷(文)
【标注】
-
求 $\sin \angle CED$ 的值;标注答案$\dfrac{{\sqrt {21} }}{7}$.解析在三角形 $CDE$ 中,已知两边一角,因此可用余弦定理求出另一边,再用正弦定理求出另外两角的正弦值.如图,设 $\angle CED = \alpha $.
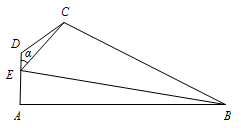 在 $\triangle CDE$ 中,由余弦定理,可得\[{EC}^2 = {CD}^2 + {DE}^2 - 2CD \cdot DE \cdot \cos \angle EDC.\]于是由题设可知,$7 = {CD}^2 + 1 + CD$,即\[{CD}^2 + CD - 6 = 0,\]解得\[CD = 2 \left(CD = - 3 < 0 , 舍去\right).\]在 $\triangle CDE$ 中,由正弦定理,可得\[\dfrac{EC}{\sin \angle EDC} = \dfrac{CD}{\sin \alpha }.\]于是\[ \sin \alpha = \dfrac{{CD \cdot \sin \frac{{2{\mathrm \pi} }}{3}}}{EC} = \dfrac{{\sqrt {21} }}{7},\]即\[\sin \angle CED = \dfrac{{\sqrt {21} }}{7}.\]
在 $\triangle CDE$ 中,由余弦定理,可得\[{EC}^2 = {CD}^2 + {DE}^2 - 2CD \cdot DE \cdot \cos \angle EDC.\]于是由题设可知,$7 = {CD}^2 + 1 + CD$,即\[{CD}^2 + CD - 6 = 0,\]解得\[CD = 2 \left(CD = - 3 < 0 , 舍去\right).\]在 $\triangle CDE$ 中,由正弦定理,可得\[\dfrac{EC}{\sin \angle EDC} = \dfrac{CD}{\sin \alpha }.\]于是\[ \sin \alpha = \dfrac{{CD \cdot \sin \frac{{2{\mathrm \pi} }}{3}}}{EC} = \dfrac{{\sqrt {21} }}{7},\]即\[\sin \angle CED = \dfrac{{\sqrt {21} }}{7}.\] -
求 $BE$ 的长.标注答案$4\sqrt 7$.解析在三角形 $AEB$ 中,已知一边一角,因此在任意知道该三角形中的一个条件,即可求出 $BE$,根据题中条件 $\angle BEC$ 和 $\angle CED$,可锁定求解 $\angle AEB$.由题设可得 $0 < \alpha < \dfrac{{{\mathrm \pi} }}{3}$,于是由(1)知\[ \cos \alpha \overset{\left[a\right]}= \sqrt {1 - {{\sin }^2}\alpha } = \dfrac{2\sqrt 7 }{7}, \](推导中用到[a])
而 $\angle AEB = \dfrac{{2{\mathrm \pi} }}{3} - \alpha $,所以\[\begin{split}\cos \angle AEB & = \cos \left( {\dfrac{{2{\mathrm \pi} }}{3} - \alpha } \right)
\\& \overset{\left[a\right]}= \cos \dfrac{{2{\mathrm \pi} }}{3}\cos \alpha + \sin \dfrac{{2{\mathrm \pi} }}{3}\sin \alpha
\\&= - \dfrac{1}{2}\cos \alpha + \dfrac{\sqrt 3 }{2}\sin \alpha
\\&= \dfrac{\sqrt 7 }{14},\end{split}\](推导中用到[a])
在 ${\mathrm{Rt}}\triangle EAB$ 中,$\cos \angle AEB = \dfrac{EA}{BE} = \dfrac{2}{BE}$,所以\[BE = \dfrac{2}{\cos \angle AEB} = 4\sqrt 7.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2