如图,$O$ 为坐标原点,双曲线 ${C_1}:\dfrac{x^2}{a_1^2} - \dfrac{y^2}{b_1^2} = 1\left({a_1} > 0,{b_1} > 0\right)$ 和椭圆 ${C_2}:\dfrac{y^2}{a_2^2} + \dfrac{x^2}{b_2^2} = 1\left({a_2} > {b_2} > 0\right)$ 均过点 $P\left(\dfrac{2\sqrt 3 }{3},1\right)$,且以 ${C_1}$ 的两个顶点和 ${C_2}$ 的两个焦点为顶点的四边形是面积为 $ 2 $ 的正方形.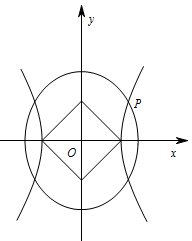
【难度】
【出处】
无
【标注】
-
求 ${C_1}$,${C_2}$ 的方程;标注答案双曲线 ${C_1}$ 方程为 ${x^2} - \dfrac{y^2}{3} = 1$;
椭圆 $C_2$ 的方程为 $\dfrac{y^2}{3} + \dfrac{x^2}{2} = 1$解析本题考查圆锥曲线的基本量.设 ${C_2}$ 的焦距为 $2{c_2}$,由题可得 $2{c_2} = 2$,$2{a_1} = 2$,从而\[{a_1} = 1,{c_2} = 1,\]因为点 $P\left( {\dfrac{2\sqrt 3 }{3},1} \right)$ 在双曲线${x^2} - \dfrac{y^2}{b_1^2} = 1$ 上,所以\[{\left( {\dfrac{2\sqrt 3 }{3}} \right)^2} - \dfrac{1}{b_1^2} = 1,\]整理,得\[b_1^2 = 3,\]由椭圆的定义可得\[2{a_2} = \sqrt {{{\left( {\dfrac{2\sqrt 3 }{3}} \right)}^2} + {{\left( {1 - 1} \right)}^2}} + \sqrt {{{\left( {\dfrac{2\sqrt 3 }{3}} \right)}^2} + {{\left( {1 + 1} \right)}^2}} = 2\sqrt 3,\]于是\[{a_2} = \sqrt 3 , b_2^2 = a_2^2 - c_2^2 = 2,\]因此,双曲线 ${C_1}$ 的方程为 ${x^2} - \dfrac{y^2}{3} = 1$;椭圆 $C_2$ 的方程为 $\dfrac{y^2}{3} + \dfrac{x^2}{2} = 1$. -
是否存在直线 $l$,使得 $l$ 与 ${C_1}$ 交于 $A$,$B$ 两点,与 ${C_2}$ 只有一个公共点,且 $ \left|\overrightarrow {OA} + \overrightarrow {OB} \right| = \left|\overrightarrow {AB} \right|$?证明你的结论.标注答案不存在.解析根据向量的平行四边形法则将 $ \left|\overrightarrow {OA} + \overrightarrow {OB} \right| = \left|\overrightarrow {AB} \right|$ 转化为 $\overrightarrow{OA}\perp\overrightarrow{OB}$ 是本题的关键.不存在符合题设条件的直线.
(i)若直线 $l$ 垂直于 $x$ 轴,因为 $l$ 与 ${C_2}$ 只有一个公共点,所以直线 $ l $ 的方程为\[x = \sqrt 2 或 x = - \sqrt 2 ,\]当 $x = \sqrt 2 $ 时,易知 $A\left( {\sqrt 2 ,\sqrt 3 } \right)$,$B\left( {\sqrt 2 , - \sqrt 3 } \right),$ 所以\[\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = 2\sqrt 2 ,\left| {\overrightarrow {AB} } \right| = 2\sqrt 3,\]此时\[\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| \ne \left| {\overrightarrow {AB} } \right|.\]当 $x = - \sqrt 2 $ 时,同理可得 $\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| \ne \left| {\overrightarrow {AB} } \right|$.
(ii)当直线 $l$ 不垂直于 $x$ 轴,设 $l$ 的方程为 $y = kx + m$,联立直线与双曲线方程\[\begin{cases}
y = kx + m, \\
{x^2} - \dfrac{y^2}{3} = 1, \\
\end{cases}\]整理,得\[\left( {3 - {k^2}} \right){x^2} - 2kmx - {m^2} - 3 = 0,\]当 $l$ 与 ${C_1}$ 相交于 $A$,$B$ 两点时,设 $A\left( {{x_1},{y_1}} \right)$,$B\left( {{x_2},{y_2}} \right)$,则 ${x_1}$,${x_2}$ 是上述方程的两个实根,从而\[\begin{cases}{x_1} + {x_2} = \dfrac{2km}{3 - k^2}, \\ {x_1}{x_2} = \dfrac{{m^2} + 3}{k^2 - 3}.\end{cases}\]于是\[\begin{split}{y_1}{y_2} & = {k^2}{x_1}{x_2} + km\left( {{x_1} + {x_2}} \right) + {m^2} \\& = \dfrac{{3{k^2} - 3{m^2}}}{{{k^2} - 3}},\end{split}\]联立直线与椭圆方程,得\[\begin{cases}y = kx + m ,\\
\dfrac{y^2}{3} + \dfrac{x^2}{2} = 1.\\
\end{cases}\]整理,得\[\left( {2{k^2} + 3} \right){x^2} + 4kmx + 2{m^2} - 6 = 0,\]因为直线 $l$ 与 ${C_2}$ 只有一个公共点,所以上述方程的判别式\[\Delta = 16{k^2}{m^2} - 8\left( {2{k^2} + 3} \right)\left( {{m^2} - 3} \right) = 0,\]化简可得\[2{k^2} = {m^2} - 3.\]因此\[\begin{split}\overrightarrow {OA} \cdot \overrightarrow {OB} & \overset{\left[a\right]}= {x_1}{x_2} + {y_1}{y_2} \\& = \dfrac{{{m^2} + 3}}{{{k^2} - 3}} + \dfrac{{3{k^2} - 3{m^2}}}{{{k^2} - 3}} \\& = \dfrac{{ - {k^2} - 3}}{{{k^2} - 3}} \ne 0,\end{split}\](推导中用到[a])
于是\[{\overrightarrow {OA} ^2} + {\overrightarrow {OB} ^2} + 2\overrightarrow {OA} \cdot \overrightarrow {OB} \ne {\overrightarrow {OA} ^2} + {\overrightarrow {OB} ^2} - 2\overrightarrow {OA} \cdot \overrightarrow {OB} ,\]即\[{\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right|^2} \ne {\left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|^2},\]所以\[\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| \ne \left| {\overrightarrow {AB} } \right|,\]综合(i)(ii)可知,不存在符合题目条件的直线.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2