如图,三棱锥 $P-ABC$ 中,$平面PAC\perp 平面ABC$,$\angle ABC=\dfrac{\mathrm \pi} {2}$,点 $D$,$E$ 在线段 $AC$ 上,且 $AD=DE=EC=2$,$PD=PC=4$,点 $F$ 在线段 $AB$ 上,且 $EF\parallel BC$.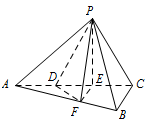

【难度】
【出处】
无
【标注】
-
证明:$AB\perp 平面PFE$;标注答案略.解析本题证明 $AB$ 分别与 $PE$ 和 $EF$ 垂直即可.由 $DE=EC$,$PD=PC$ 知,$E$ 为等腰 $\triangle PDC$ 中 $DC$ 边的中点,故 $PE\perp AC$.
又 $平面PAC\perp 平面ABC$,$平面PAC\cap 平面ABC=AC$,$PE\subset 平面PAC$,$PE\perp AC$,
所以 $PE\perp 平面ABC$,从而 $PE\perp AB$.
因为 $\angle ABC=\dfrac{\mathrm \pi} {2}$,$EF\parallel BC$,所以 $AB\perp EF$.
从而 $AB$ 与平面 $PFE$ 内两条相交直线 $PE$,$EF$ 都垂直,
所以 $AB\perp 平面PFE$. -
若四棱锥 $P-DFBC$ 的体积为 $7$,求线段 $BC$ 的长.标注答案$BC=3$ 或 $BC=3\sqrt 3$.解析在求四棱锥 $P-DFBC$ 的底面 $DFBC$ 的面积时,我们用 $\triangle ABC$ 的面积减去 $\triangle ADF$ 的面积即可.设 $BC=x$,则在 $\mathrm {Rt}\triangle ABC$ 中,\[AB=\sqrt{AC^2-BC^2}=\sqrt{36-x^2},\]从而\[S_{\triangle ABC}=\dfrac 12 AB\cdot BC=\dfrac 12x\sqrt{36-x^2}.\]因为 $EF\parallel BC$,所以 $\triangle AFE\backsim \triangle ABC$,$\dfrac{AF}{AB}=\dfrac{AE}{AC}=\dfrac 23$,故 $\dfrac{S_{\triangle AFE}}{S_{\triangle ABC}}=\left(\dfrac 23\right)^2=\dfrac 49$,即\[S_{\triangle AFE}=\dfrac 49 S_{\triangle ABC}.\]因为 $AD=\dfrac 12AE$,所以\[\begin{split}S_{\triangle AFD}&=\dfrac 12S_{\triangle AFE}\\&=\dfrac 12\times \dfrac 49S_{\triangle ABC}\\&=\dfrac 29S_{\triangle ABC}\\&=\dfrac 19x\sqrt{36-x^2},\end{split}\]从而四边形 $DFBC$ 的面积为\[S_{四边形DFBC}=S_{\triangle ABC}-S_{\triangle AFD}=\dfrac{7}{18}x\sqrt{36-x^2}.\]由(1)知 $PE\perp 平面ABC$,所以 $PE$ 为四棱锥$P-DFBC$ 的高.
在 $\mathrm {Rt}\triangle PEC$ 中,$PE=\sqrt{PC^2-EC^2}=\sqrt{4^2-2^2}=2\sqrt 3$,根据棱锥体积公式可得\[V_{四棱锥P-DFBC}=\dfrac 13S_{四边形DFBC}\cdot PE=\dfrac 13\times\dfrac{7}{18}x\sqrt{36-x^2}\times 2\sqrt 3=7,\]所以 $x^4-36x^2+243=0$,解得 $x^2=9$ 或 $x^2=27$.由于 $x>0$,因此 $x=3$ 或 $x=3\sqrt 3$.所以 $BC=3$ 或 $BC=3\sqrt 3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2