如图，椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\left(a>b>0\right)$ 的左、右焦点分别为 $F_1$，$F_2$，过 $F_2$ 的直线交椭圆于 $P$，$Q$ 两点，且 $PQ\perp PF_1$．
【难度】
【出处】
无
【标注】
-
若 ${\left|{PF_1}\right|}=2+\sqrt 2$，${\left|{PF_2}\right|}=2-\sqrt 2$，求椭圆标准方程；标注答案$\dfrac{x^2}{4}+y^2=1$．解析根据所给条件，利用椭圆定义可得 $a$ 值，在 $\triangle PF_1F_2$ 中应用勾股定理可求得 $c$ 值．由椭圆的定义，$2a={\left|{PF_1}\right|}+{\left|{PF_2}\right|}=\left(2+\sqrt 2\right)+\left(2-\sqrt 2\right)=4$，故 $a=2$．
设椭圆的半焦距为 $c$，由于 $PF_1\perp PF_2$，
因此 $2c={\left|{F_1F_2}\right|}=\sqrt{{\left|{PF_1}\right|^2}+{\left|{PF_2}\right|}^2}=\sqrt{\left(2+\sqrt 2\right)^2+\left(2-\sqrt 2\right)^2}=2\sqrt 3$，
即 $c=\sqrt 3$，从而 $b=\sqrt{a^2-c^2}=1$，
故所求椭圆的标准方程为 $\dfrac{x^2}{4}+y^2=1$． -
若 ${\left|{PQ}\right|}=\lambda {\left|{PF_1}\right|}$，且 $\dfrac 34\leqslant \lambda<\dfrac 43$，试确定椭圆离心率 $e$ 的取值范围．标注答案$\dfrac{\sqrt 2}{2}<e\leqslant \dfrac{\sqrt 5}{3}$．解析本题需建立 $\lambda$ 和离心率 $e$ 的关系，然后根据 $\lambda$ 的取值范围求出 $e$ 的取值范围．具体可先根据椭圆定义将 $\left|PF_1\right|$ 和 $\left|PF_2\right|$ 用 $\lambda$ 和半长轴长 $a$ 表示出来，然后在 $\mathrm {Rt}\triangle PF_1F_2$ 中应用勾股定理建立起 $a,c,\lambda$ 的数量关系，继而得到 $e$ 与 $\lambda$ 的关系．
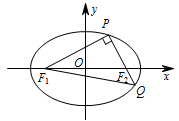如图所示，由 $PF_1\perp PQ$，${\left|{PQ}\right|}=\lambda {\left|{PF_1}\right|}$，得 ${\left|{QF_1}\right|}=\sqrt{{\left|{PF_1}\right|}^2+{\left|{PQ}\right|}^2}=\sqrt{1+\lambda^2}{\left|{PF_1}\right|}$．
由椭圆的定义，${\left|{PF_1}\right|}+{\left|{PF_2}\right|}=2a$，${\left|{QF_1}\right|}+{\left|{QF_2}\right|}=2a$，知 ${\left|{PF_1}\right|}+{\left|{PQ}\right|}+{\left|{QF_1}\right|}=4a$．
于是 $\left(1+\lambda+\sqrt{1+\lambda^2}\right){\left|{PF_1}\right|}=4a$，
解得 ${\left|{PF_1}\right|}=\dfrac{4a}{1+\lambda+\sqrt{1+\lambda^2}}$，
故 ${\left|{PF_2}\right|}=2a-{\left|{PF_1}\right|}=\dfrac{2a\left(\lambda+\sqrt{1+\lambda^2}-1\right)}{1+\lambda+\sqrt{1+\lambda^2}}$．
由勾股定理得 ${\left|{PF_1}\right|}^2+{\left|{PF_2}\right|}^2={\left|{F_1F_2}\right|}^2=\left(2c\right)^2=4c^2$，
从而 $\left(\dfrac{4a}{1+\lambda+\sqrt{1+\lambda^2}}\right)^2+\left[\dfrac{2a\left(\lambda+\sqrt{1+\lambda^2}-1\right)}{1+\lambda+\sqrt{1+\lambda^2}}\right]^2=4c^2$．
两边除以 $4a^2$，得 $\dfrac{4}{\left(1+\lambda+\sqrt{1+\lambda^2}\right)^2}+\dfrac{\left(\lambda+\sqrt{1+\lambda^2}-1\right)^2}{\left(1+\lambda+\sqrt{1+\lambda^2}\right)^2}=e^2$．
若记 $t=1+\lambda+\sqrt{1+\lambda^2}$，则上式变成 $e^2=\dfrac{4+\left(t-2\right)^2}{t^2}=8\left(\dfrac 1t-\dfrac 14\right)^2+\dfrac 12$．
由 $\dfrac 34\leqslant \lambda <\dfrac 43$，并注意到 $t=1+\lambda+\sqrt{1+\lambda^2}$ 关于 $\lambda$ 的单调性，
得 $3\leqslant t<4$，即 $\dfrac 14<\dfrac 1t\leqslant \dfrac 13$，进而 $\dfrac 12<e^2\leqslant \dfrac 59$，即 $\dfrac{\sqrt 2}{2}<e\leqslant \dfrac{\sqrt 5}{3}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
