略

有关弦的中点问题，设出弦的两个端点的坐标，利用点差法可得直线 $OM$ 的斜率与 $l$ 的斜率的关系．用点差法来证．
设 $A\left(x_1,y_1\right)$，$B\left(x_2,y_2\right)$，则：
$ x_M=\dfrac{x_1+x_2}{2} $，$ y_{M}=\dfrac{y_1+y_2}{2} $，所以 $ k_{OM}=\dfrac{y_{M}}{x_{M}}=\dfrac{y_1+y_2}{x_1+x_2} $．
又\[ \begin{cases}9x_1^2+y_1^2=m^2,\\9x_2^2+y_2^2=m^2,\end{cases}\]两式相减得\[9\left(x_1+x_2\right)\left(x_1-x_2\right)+\left(y_1+y_2\right)\left(y_1-y_2\right)=0, \]即\[ \dfrac{y_1+y_2}{x_1+x_2}\cdot\dfrac{y_1-y_2}{x_1-x_2}=-9. \]所以 $k_{OM}\cdot k_l=-9 $，
因此原命题得证，且定值为 $-9$．

四边形 $OAPB$ 能为平行四边形，此时 $l$ 的斜率为 $4\pm\sqrt7$

设出中点坐标，以中点坐标为参数驱动图形，再结合第一小题的结论进行消参．假设存在符合题意的平行四边形 $OAPB$，如图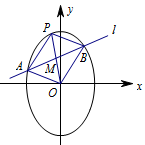．设 $M\left(x_0,y_0\right)$，则 $P\left(2x_0,2y_0\right)$，于是\[ 9x_0^2+y_0^2=\dfrac 14m^2 \quad \cdots \cdots ① . \]此时根据第（1）小题的结论，由斜率公式有\[ \dfrac{m-y_0}{\dfrac m3-x_0}\cdot\dfrac{y_0}{x_0}=-9, \]整理得\[ 3mx_0+my_0=9x_0^2+y_0^2=\dfrac 14m^2, \]即\[ 3x_0+y_0=\dfrac 14m \quad \cdots \cdots ② . \]由方程 ① 与 ② 解得\[ \begin{cases}x_0=\dfrac{m}{24}\left(1+\sqrt 7\right),\\y_0=\dfrac{m}{8}\left(1-\sqrt 7\right),\end{cases} \]或\[ \begin{cases}x_0=\dfrac{m}{24}\left(1-\sqrt 7\right),\\y_0=\dfrac{m}{8}\left(1+\sqrt 7\right),\end{cases} \]所以 $ k_{OM}=\dfrac{y_0}{x_0}=\dfrac{3\left(1-\sqrt7\right)}{1+\sqrt7} $ 或 $ k_{OM}=\dfrac{y_0}{x_0}=\dfrac{3\left(1+\sqrt7\right)}{1-\sqrt7} $，
于是根据第（1）小题的结论，得直线 $l$ 的斜率为\[ -9\cdot\dfrac{x_0}{y_0}=4+\sqrt 7. \]或\[ -9\cdot\dfrac{x_0}{y_0}=4-\sqrt 7. \]故当直线 $l$ 的斜率为 $4\pm\sqrt7$ 时，四边形 $OAPB$ 为平行四边形．