如图,四边形 $ABCD$ 为菱形,$G$ 为 $AC$ 与 $BD$ 的交点,$BE\perp 平面ABCD$.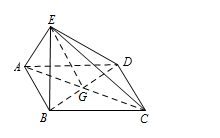

【难度】
【出处】
2015年高考全国Ⅰ卷(文)
【标注】
-
证明:$平面AEC\perp 平面BED$;标注答案略解析面面垂直的证明关键在于证明面上一条直线垂直于另一个平面因为四边形 $ABCD$ 为菱形,所以 $AC\perp BD$.
因为 $BE\perp 平面ABCD$,所以 $AC\perp BE$.
因为 $BD\cap BE=B $,所以 $AC\perp 平面BED$.
又 $AC\subset 平面AEC$,所以 $平面AEC\perp 平面BED$. -
若 $\angle ABC=120^\circ$,$AE\perp EC$,三棱锥 $E-ACD$ 的体积为 $\dfrac{\sqrt6}{3}$,求该三棱锥的侧面积.标注答案$3+2\sqrt 5$解析利用已知三棱锥的体积计算出几何体各边长度,然后分别计算侧面积.设 $AB=x$.
在菱形 $ABCD$ 中,由 $\angle ABC=120^\circ$,可得 $ \triangle{BCD} $ 和 $\triangle{ABD}$ 均是边长为 $x$ 的等边三角形.
所以 $AG=GC=\dfrac{\sqrt 3}{2}x$,$GB=GD=\dfrac{x}{2}$.
因为 $AE\perp EC$,所以在 $\mathrm{Rt}\triangle AEC$ 中,\[EG=\dfrac{1}{2}AC=\dfrac{\sqrt 3}{2}x.\]由 $BE\perp 平面ABCD$,得 $BE\perp BD$,所以 $\triangle EBG$ 为直角三角形,可得\[BE=\sqrt{{EG}^2-{BG}^2}=\dfrac{\sqrt 2 }{2}x.\]所以三棱锥 $E-ACD$ 的体积\[\begin{split}V_{E-ACD}&\overset{\left[a\right]}=\dfrac{1}{3}\cdot \dfrac{1}{2}\cdot AC\cdot GD\cdot BE\\&=\dfrac{\sqrt 6}{24}x^3\\&=\dfrac{\sqrt 6}{3},\end{split}\](推导中用到:$\left[a\right]$)
故 $x=2$.
从而可得\[AE=EC=ED=\sqrt{{AB}^2+{BE}^2}=\sqrt 6.\]所以\[S_{\triangle EAC}=\dfrac 12 \cdot AE\cdot EC=3.\]因为 $\triangle EAD$ 与 $\triangle ECD$ 是全等的三角形,所以\[S_{\triangle EAD}=S_{\triangle ECD}=\sqrt 5.\]故三棱锥 $E-ACD$ 的侧面积为 $3+2\sqrt 5$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2