如图，$AB$ 是 $\odot O$ 的直径，$AC$ 是 $\odot O$ 的切线，$BC$ 交 $\odot O$ 于点 $E$．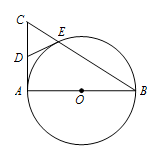
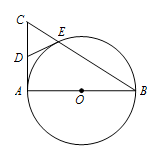
【难度】
【出处】
2015年高考全国Ⅰ卷（文）
【标注】
-
若 $D$ 为 $AC$ 的中点，证明：$DE$ 是 $\odot O$ 的切线；标注答案略解析通过证明 $\triangle AOD$ 和 $\triangle EOD$ 全等来解决问题．连接 $AE$，$ OD $，$ OE$，如图所示：
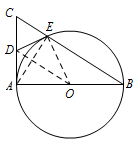由 $AB$ 是直径可知\[AE\perp BC.\]所以 $ \triangle AEC$ 是直角三角形，且 $\angle AEC=90^\circ$．
又 $D$ 为 $AC$ 中点，所以\[DA=DE.\]又 $A$、$E$ 在 $\odot O$ 上，所以\[ OA=OE,\]又 $ OD=OD $，所以\[\triangle AOD\cong \triangle EOD, \]所以\[ \angle OED=\angle OAD=90^\circ ,\]所以\[OE\perp DE ,\]所以 $ DE$ 是 $\odot O$ 的切线． -
若 $OA=\sqrt{3}CE$，求 $\angle ACB$ 的大小．标注答案$60^\circ$解析利用切割线定理可知 $CE\cdot CB=CA^2.$ 结合 $\mathrm {Rt}\triangle ABC$ 的勾股定理解决问题．由 $OA=\sqrt 3CE$，知\[AB=2\sqrt 3CE.\]由 $CB$ 为圆的割线，$CA$ 为圆的切线，知\[CE\cdot CB\overset{\left[a\right]}=CA^2.\]（推导中用到：$\left[a\right]$）
在 $\mathrm {Rt}\triangle ABC$ 中，\[CA^2=CB^2-AB^2,\]所以\[ \dfrac{AB}{2\sqrt 3}\cdot CB=CB^2-AB^2,\]整理，得\[\left(\sqrt 3CB-2AB\right)\left(2CB+\sqrt 3AB\right)=0,\]所以\[ \dfrac{AB}{CB}=\dfrac{\sqrt 3}{2}=\sin \angle ACB.\]又 $\angle ACB$ 为锐角，所以 $ \angle ACB=60^\circ$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
